Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 96

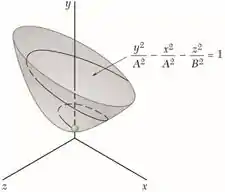
O movimento tridimensional de uma partícula é definido pelo vetor de posição r = (At cos t)i + (A t 2 + 1 )j + (Bt sen t)k, onde r e t estão expressos em metros e segundos, respectivamente. Mostre que a curva descrita pela partícula cai sobre o hiperboloide (y/A)2 - (x/A)2 - (z/B)2 = 1. Para A = 3 e B = 1, determine (a) as intensidades da velocidade e aceleração quando t = 0 e (b) o menor valor de t diferente de zero para o qual o vetor de posição e o vetor de velocidade são perpendiculares entre si.

Passo 1

Partiu mais uma questão de resmat? O exercício pede que a gente determine as intensidades da velocidade e aceleração quando t = 0 e (b) o menor valor de t diferente de zero para o qual o vetor de posição e o vetor de velocidade são perpendiculares entre si.

Nós temos

r = A t cos ⁡ t i + A t 2 + 1 j + b t sin ⁡ t k

ou

x = A t cos ⁡ t             y = A t 2 + 1             z = B t sin ⁡ t

Então

cos 2 = x A t           sin ⁡ t = z B t             t 2 = y A 2 = 1

Agora

cos 2   t + sin 2   t = 1 ⇒ x A t 2 + z B t 2 = 1

ou

t 2 = x A 2 + z B 2

Então

y A 2 - 1 = x A 2 + z B 2

Passo 2

  1. Com A = 3 e B = 1, temos

    2. v = d r d t = 3 cos ⁡ t - t sin ⁡ t i + 3 t t 2 + 1 j + sin ⁡ t + t cos ⁡ t k

    e

    a = d v d t = 3 - sin ⁡ t - sin ⁡ t - t cos ⁡ t i + 3 t 2 + 1 - t t t 2 + 1 t 2 + 1 j

    + cos ⁡ t + cos ⁡ t - t sin ⁡ t k = - 3 2 sin ⁡ t + t cos ⁡ t i + 3 1 t 2 + 1 3 / 2 j + 2 cos ⁡ t - t sin ⁡ t k

    Em t = 0:

    v = 3 1 - 0 i + 0 j + 0 k

    v = v x 2 + v y 2 + v z 2

    e

    a = - 3 0 i + 3 1 j + 2 - 0 k

    Então

    a 2 = 0 2 + 3 2 + 2 2 = 13

    Passo 3

  2. Se r e v são perpendiculares, r ∙ v = 0

3 t cos ⁡ t i + 3 t 2 + 1 j + t sin ⁡ t k ∙ 3 cos ⁡ t - t sin ⁡ t i + 3 t t 2 + 1 j + sin ⁡ t + t cos ⁡ t k = 0

ou

3 t cos ⁡ t 3 cos ⁡ t - t sin ⁡ t + 3 t 2 + 1 3 t t 2 + 1 + t sin ⁡ t sin ⁡ t + t cos ⁡ t = 0

Expandindo

9 t   cos 2   t - 9 t 2 sin ⁡ t cos ⁡ t + 9 t + t   sin 2   t + t 2 sin ⁡ t cos ⁡ t = 0

ou (com t ≠ 0)

10 + 8   cos 2   t - 8 t sin ⁡ t cos ⁡ t = 0

ou

7 + 2 cos ⁡ 2 t - 2 t sin ⁡ 2 t = 0

Resposta

a)  v = 3   ft/s

a = 3.61   ft/ s 2

b) Usando "tentativa e erro" ou métodos numéricos, a menor raiz é  t = 3.82   s

N o t a :   A próxima raiz é   t = 4.38   s.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A velocidade inicial v0 de um disco de hockey é de 168 km/h. Determine (a) o maior valor (menor que 45°) do ângulo α que o disco entrará na rede e (b) o tempo correspondente necessário para o disco at
Um alpinista planeja pular de A para B sobre uma fenda. Determine o menor valor da velocidade inicial do alpinista v0 e o valor correspondente do ângulo α para que ele caia em B.
Determine a velocidade necessária da correia B se a velocidade relativa com a qual a areia atinge a correia B é (a) vertical, (b) a menor possível.
Os aviões A e B estão voando à mesma altitude e acompanhando o olho de um furacão C. A velocidade relativa de C em relação a A é vC/A = 235 km/h 40°. Determine (a) a velocidade relativa de B em relaçã
Um radar costeiro indica que uma barca sai de seu atracadouro com uma velocidade v = 18,5 km/h 70°, enquanto instrumentos a bordo da barca indicam velocidade de 19 km/h e direção 30° a oeste da direçã