Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 128

Determine a velocidade necessária da correia B se a velocidade relativa com a qual a areia atinge a correia B é (a) vertical, (b) a menor possível.

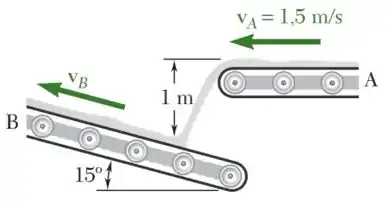
Passo 1

O graõ de areia vai passar por um movimento projetado.

v s x = v s x 0 = c o n s t a n t e = - 1,5   m / s

direção-y.

v s y = 2 g h = ( 2 ) ( 9,81   m / s ² ) ( 1 m ) = 4,42   m / s ↓

Passo 2

Relativa a velocidade.

(a)Se v S / B é vertical,

- v S / B j = - 5 i - 13.9 j - ( v B cos ⁡ 15 i + v B   s e n   15 j )

= - 5 i - 13.9 j + v B cos ⁡ 15 i - v B   s e n   15 j

Passo 3

Equalize os componentes

i : 0 = - 5 + v B cos ⁡ 15 °                 v B = 5 cos ⁡ 15 ° = 5.176   m / s

v B = 5.18   m / s ∡ 15 °

Passo 4

(b) v S / C é menor possivel, então faça v S / B   ⊥ a   v B   e m   1 .

- v S / B s e n   15 ° i - v S / B c o s   15 ° j = - 5 i -   13.9 j + v B   c o s   15 ° i - v B   s e n   15 ° j

Equalizando os componentes e transpondo os termos.

( s e n   15 ° ) v S / B   + ( c o s   15 ° ) v B = 5

( c o s   15 ° ) v S / B   + ( s e n   15 ° ) v B = 13.90

Resolvendo

v S / B = 14.72 3 / s                               v B = 1.232 3 / s

Resposta

a :   v B = 5.18   m / s ∡ 15 °

b :   v B = 1.232   m / s     ∡ 15 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma motocicleta parte do repouso com uma aceleração inicial de 3 m / s 2 e a aceleração então varia com a distância s como mostrado na figura. Determine a velocidade v da motocicleta quando s = 200m .
Uma partícula oscila ao longo de uma linha reta com uma velocidade variando senoidalmente em milímetros por segundo dada por v = 16 sen ⁡ π t / 6 , onde t é em segundos. Se o deslocamento da partícula
Pequenas bolas de aço caem do repouso através da abertura em A a uma taxa constante de duas por segundo. Encontre a separação vertical h de duas bolas consecutivas quando a mais baixa tiver caído 3 me
Uma partícula se move ao longo da direção s com aceleração constante. O deslocamento, medido a partir de uma posição apropriada, é de 2m no instante t = 0 e é zero quando t = 10s . Se a velocidade da
O elevador principal A da torre CN em Toronto sobe cerca de 350m e na maior parte de seu curso tem uma velocidade constante de 22k m / h . Suponha que tanto a aceleração quanto a desaceleração tenham