Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.9 - Ex. 212
Uma nave espacial no espaço profundo está programada para aumentar sua velocidade por uma quantidade desejada através da combustão de seu motor por um determinado tempo de duração . Após vinte e cinco por cento da combustão, o motor repentinamente falha e posteriormente produz apenas metade de seu empuxo normal. Qual o percentual de v é alcançado se o motor do foguete é acionado pelo tempo programado ? Quanto tempo extra o foguete precisaria operar a fim de compensar a falha?
Passo 1
Vamos construir um gráfico que demonstre o comportamento da força em função do tempo. Vamos dividir o intervalo de a em quatro partes para se ajustar aos dados do enunciado:
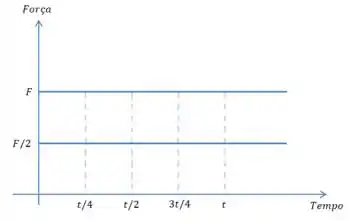
Agora vamos nos lembrar do teorema do impulso:
Perceba que essa integral da esquerda é simplesmente a área sob o gráfico!
Passo 2
Depois que o motor falha, no instante , a força cai para , e a área calculada pela integral é:
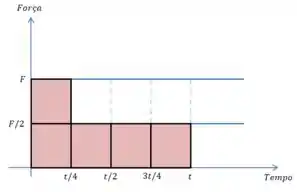
Vamos supor que é o momento fornecido quando o motor não falha, e é o fornecido quando falha:
Podemos dividir ambos os lados pela massa e obter a razão entre as variações de velocidade:
Passo 3
Para compensar essa falha, considerando que a força continue em , o motor precisa continuar operando por mais três “quadrados”.
Como cada quadrado “vale” , o tempo extra pelo qual o motor precisa operar é:
Resposta
O percentual é e o tempo extra é .