Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.9 - Ex. 204
O carro de massa é submetido à força exponencialmente descrescente, que representa um carregamento de choque ou explosivo. Se o carro está parado no instante de tempo , determine sua velocidade e deslocamento como funções do tempo. Qual é o valor de para valores elevados de ?
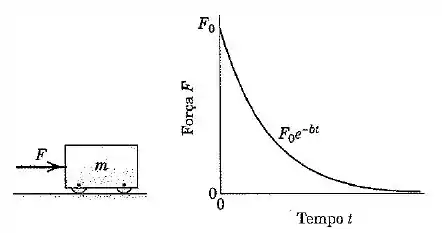
Passo 1
Vamos lembrar do teorema do impulso:
Como nesse caso o carro parte do repouso, temos , e substituindo a equação que foi dada para a força:
Vamos encontrar uma equação para a velocidade:
Daqui já podemos ver que, quando tende ao infinito, a velocidade tende a .
Passo 2
Agora precisamos transformar isso em uma equação da posição em função do tempo:
E agora podemos integrar:
E então:
Resposta
A velocidade é dada por , e tende a para valores elevados de . A posição é dada por .
Exercícios de Livros Relacionados
O poste uniforme tem uma massa de 15 kg e cai do repouso quando θ = 90 ° . Ele bate na aresta em A quando θ = 60 ° . Se o poste então começa a pivotar em torno desse ponto após o contato, determine a
Uma bola tendo uma massa de 8 kg e velocidade inicial v 1 = 0,2m / s rola sobre uma depressão de 30 mm de comprimento. Supondo que a bola rola pelas arestas de contato primeiro A, depois B, sem desliz
O centro O da roda tem uma velocidade v 1 = 2 m / s para cima na inclinação de 10 % no instante de tempo t = 0 . Encontre a velocidade v 2 da roda quando t = 6s . A roda tem um raio de giração de 90m
Uma força horizontal constante P é aplicada ao centro O do disco circular uniforme de massa m por meio do garfo leve como mostrado. O disco parte do repouso e rola por t segundos sem deslizar sobre a
A barra fina uniforme AB, de 6 kg, é submetida a uma ligeira perturbação horizontal quando está na posição vertical e gira em torno de B sem deslizar. Subsequentemente, ela atinge o degrau em C. O imp