Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.9 - Ex. 217
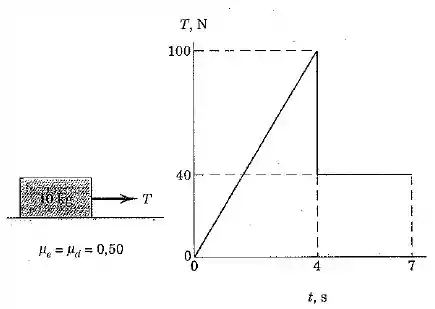
O bloco de está parado sobre a superfície horizontal quanto a força é aplicada a ele por segundos. A variação de com o tempo é apresentada. Calcule a velocidade máxima atingida pelo bloco e o intervalo de tempo total durante o qual o bloco está em movimento. Os coeficientes de atrito estático e dinâmico são ambos .
Passo 1
Bom galera, nesse exercício queremos encontrar a velocidade máxima atingida pelo bloco e o intervalo de tempo. O bloco começa a se mover em
Ocorre no tempo
Passo 2
Por definição, temos que
Sabemos que no tempo temos sua velocidade máxima, substituindo então temos
Passo 3
Quando , temos
Isolando ficamos com
Resposta
Exercícios de Livros Relacionados
O bloco de 10k g está se deslocando para a esquerda com uma velocidade de 1,2m / s no instante de tempo t = 0 , quando a força P é aplicada como mostrado no gráfico. A força continua no nível de 10N .
O sistema hidráulico dos freios para o caminhão e o reboque são regulados para produzir forças de frenagem iguais para as duas unidades. Se os freios são aplicados de maneira uniforme por 5 segundos p
O carro B ( 1500k g ) viajando para oeste a 48k m / h colide com o carro A ( 1600k g ) viajando para o norte 32k m / h conforme indicado. Se os dois carros ficam presos e se deslocam em conjunto como
O carro B está inicialmente parado e é atingido pelo carro A que se desloca com velocidade inicial v 1 = 30k m / h . Os carros ficam presos e se deslocam juntos com velocidade v ' após a colisão. Se o
O carro de massa m é submetido à força F exponencialmente descrescente, que representa um carregamento de choque ou explosivo. Se o carro está parado no instante de tempo t = 0 , determine sua velocid