Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 157

Determine o sistema força-binário em O , que seja equivalente às duas forças aplicadas ao eixo A O B . R → é perpendicular a M → O ?

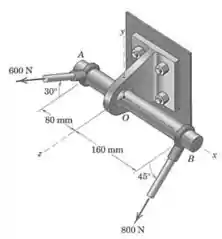
Passo 1

Vamos começar escrevendo as duas forças em forma vetorial:

F → 1 = - 800 sen ⁡ 45 ° j ^ + 800 cos ⁡ 45 °   k ^

F → 2 = 600 sen ⁡ 30 °   j ^ + 600 cos ⁡ 30 °   k ^ N m

E então a força resultante é:

R → = F → 1 + F → 2

R → = - 800 sen ⁡ 45 ° + 600 sen ⁡ 30 ° j ^ + 800 cos ⁡ 45 ° + 600 cos ⁡ 30 ° k ^

R → = - 266   j ^ + 1085   k ^   N

Passo 2

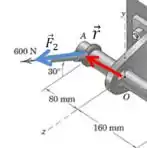
Agora vamos calcular o momento de cada uma das forças usando a definição de momento:

M → = r → × F →

M → 1 = r → × F → 1

M → 1 = 0,160   i ^ × - 800 sen ⁡ 45 ° j ^ + 800 cos ⁡ 45 °   k ^

M → 1 = i ^ j ^ k ^ 0,160 0 0 0 - 566 566

M → 1 = - 566 0,160 k ^ - 566 0,160 j ^

M → 1 = - 90,56   j ^ - 90,56   k ^   N m

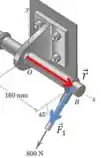
Passo 3

Agora vamos fazer o mesmo para a outra força:

M → 2 = r → × F → 2

M → 2 = - 0,080   i ^ × 600 sen ⁡ 30 °   j ^ + 600 cos ⁡ 30 °   k ^

M → 2 = i ^ j ^ k ^ - 0,080 0 0 0 300 520

M → 2 = - 0,080 300 k ^ - ( - 0,080 ) ( 520 ) ( j ^ )

M → 2 = 41,6   j ^ - 24   k ^   N m

Agora podemos somar os momentos:

M → = M → 1 + M → 2

M → = - 90,56   j ^ - 90,56   k ^ + 41,6   j ^ - 24   k ^

M → = - 48,9   j ^ - 114   k ^   N m

Passo 4

Por últimos queremos saber se R → é perpendicular a M → . A melhor forma de fazer isso é verificar se o produto interno é nulo:

R → ∙ M → = - 266   j ^ + 1085   k ^   ∙ - 48,9   j ^ - 114   k ^

R → ∙ M → = - 266 - 48,9 + ( 1085 ) ( - 114 )

R → ∙ M → = - 110,6

E como o resultando não é zero, os dois vetores não são perpendiculares.

Resposta

A força é R → = - 266   j ^ + 1085   k ^   N , o momento é M → = - 48,9   j ^ - 114   k ^   N m e os dois vetores não são perpendiculares.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A carga em A cria uma força de 200 N no arame A B . Expresse essa força como um vetor cartesiano, agindo sobre A e direcionada para B .
2.143 Os três cabos de suporte exercem as forças mostradas na figura. Represente cada força como um vetor unitário.
Se F 1 = 100 i - 120 j + 75 kN e F 2 = - 2 00 i + 25 0 j + 100 kN , determine o momento resultante produzido por essas forças em relação ao ponto O . Expresse o resultado como um vetor cartesiano.
Determine o momento da força F em relação ao ponto O . Expresse o resultado como um vetor cartesiano.
70. Uma força vertical F = 60N é aplicada no cabo da chave inglesa. Determine o momento que essa força exerce ao longo do eixo AB (eixo x ) do encanamento. Tanto a chave quanto o encanamento ABC estão