Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 43

Uma bola tendo uma massa de 8 kg e velocidade inicial v 1 = 0,2   m / s rola sobre uma depressão de 30 mm de comprimento. Supondo que a bola rola pelas arestas de contato primeiro A, depois B, sem deslizar, determine sua velocidade final v 2 quando ela alcança o outro lado.

Passo 1

Começaremos o exercício escrevendo a velocidade angular da bola nos instantes 1 e 2 ilustrados na figura a seguir, bem como o valor do ângulo θ e da altura h:

ω 1 = 0,2 0,125 = 1,6   r a d / s

ω 2 = v 2 0,125 → ω 2 = 8 v 2

θ = s e n - 1 0,015 0,125 → θ = 6,8921 °

h = 0,125 - 0,125 c o s θ = 0,125 - 0,125 c o s ⁡ ( 6,8921 ° )

h = 0,90326   m m

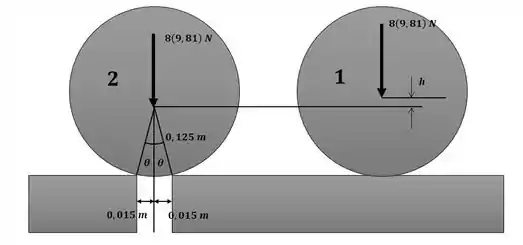
Passo 2

Agora podemos aplicar a equação da conservação da energia para os instantes 1 e 2, sendo assim:

1 2 8 0,2 2 + 1 2 2 5 8 0,125 2 1,6 2 + 0 = - 0,90326 10 - 3 8 9,81 + 1 2 8 ω 2 0,125 2 + 1 2 2 5 8 0,125 2 ω 2

ω = 1,836   r a d / s

Agora iremos aplicar a conservação da quantidade de movimento angular para os instantes 2 e 3 ao redor do ponto B, conforme ilustrado na imagem a seguir:

H B 2 = H B 3

2 5 8 0,125 2 1,836 + 8 1,836 0,125 cos ⁡ 6,892 ° 0,125 c o s 6,8962 ° - 8 0,22948 s e n 6,8962 ° 0,125 s e n 6,892 ° = 2 5 8 0,125 2 ω 3 + 8 0,125 ω 3 ( 0,125 )

ω 3 = 1,798   r a d / s

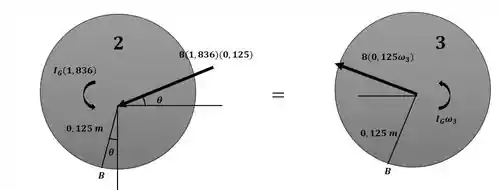
Passo 3

Agora podemos aplicar a equação da conservação da energia para os instantes 3 e 4 conforme a imagem a seguir:

T 3 + V 3 = T 4 + V 4

1 2 2 5 8 0,125 2 1,798 2 + 1 2 8 1,798 2 0,125 2 + 0 = 8 9,81 0,90326 10 - 3 + 1 2 2 5 8 0,125 2 ω 4 2 + 1 2 8 ω 4 2 0,125 2

ω 4 = 1,56   r a d / s

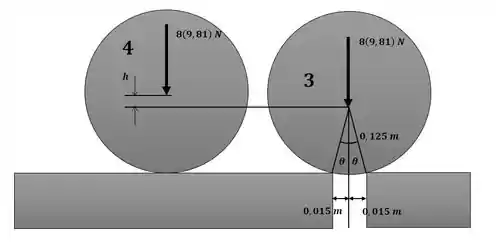
Por fim, podemos encontrar v 2 :

v 2 = 1,56 0,125 → v 2 = 0,195   m / s

Resposta

v 2 = 0,195   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que o sistema mostrado começa do repouso, encontre a velocidade em t = 1,2 s de (a) colar A, (b) colar B. Despreze as massas das polias e o efeito do atrito.
Uma balança de mola A e uma balança de alavanca B com braços de alavanca iguais estão presas ao teto de um elevador e pacotes idênticos estão sendo segurados por elas, tal como mostra a figura. Sabend
O valor da aceleração da gravidade g em qualquer latitude ϕ pode ser dado pela fórmula g = 9,7087 1 + 0,0053sen 2 ϕ m/ s 2 onde o efeito da rotação da Terra e também o fato de que a Terra não ser esfé
Para transportar uma série de feixes de telhas A para um telhado, um empreiteiro usa um elevador motorizado que consiste em uma plataforma horizontal BC que se desloca em trilhos presos às laterais de
Para descarregar uma pilha de madeira compensada de um caminhão, o motorista primeiro inclina a carroceria do caminhão e depois acelera do repouso. Saber que os coeficientes de atrito entre a folha de