Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.8 - Ex. 176
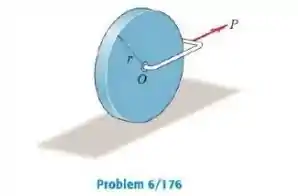
Uma força horizontal constante é aplicada ao centro do disco circular uniforme de massa por meio do garfo leve como mostrado. O disco parte do repouso e rola por segundos sem deslizar sobre a superfície horizontal. Determine a velocidade do centro em termos de .
Passo 1
Considerando que o eixo está ordenado no sentido do movimento e que momentos no sentido antihorário são positivos, temos
Pela Segunda Lei de Newton, o somatório das forças externas sobre um corpo é igual a sua taxa de variação da quantidade de movimento linear:
Mas , logo,
Na direção do movimento,
De onde tiramos que
Passo 2
Para a quantidade de movimento angular, temos
Neste problema ficamos com
De onde tiramos que
Passo 3
Igualando as duas expressões obtidas para , achamos
Isolando , obtemos
Resposta
Exercícios de Livros Relacionados
As hélices de um navio de peso W podem produzir uma força propulsora Fo; eles produzem uma força de mesma magnitude, mas de direção oposta quando os motores são invertidos. Sabendo que o navio estava
As caixas A e B estão paradas em uma esteira que está inicialmente em repouso. A correia é repentinamente iniciada em uma direção para cima de modo que o deslizamento ocorra entre a correia e as caixa
Um jogador de hockey bate no disco de maneira que este chega ao repouso 9 s depois de ter escorregado 30 m sobre o gelo. Determine (a) a velocidade inicial do disco e (b) o coeficiente de atrito entre
Uma embalagem está em repouso em uma correia transportadora, que inicialmente está em repouso. A correia é acionada e se move para a direita por 1,3s com uma aceleração constante de 2 m/ s 2 . A corre
Uma bola de demolição B de 60 kg está presa a um cabo de aço AB de 15 m de comprimento e oscila no arco vertical mostrado na figura. Determine a tração no cabo (a) no ponto mais alto C da oscilação, (