Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 109

 16.109.  O disco está se deslocando para a esquerda de tal maneira que ele tem uma aceleração angular α = 8 r a d / s 2 e velocidade angular ω = 3 r a d / s   no instante mostrado. Se ele não desliza em A , determine a aceleração do ponto B .

Passo 1

Visto que o ponto C está localizado no centro da roda, a aceleração angular dele será diferente dos demais pontos, podemos defini-la como   α C = R ( α ) :

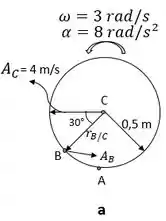
α C =   α r = 0,5(8)

α C = 4   r a d / s 2

Passo 2

O ponto B se desloca ao longo de uma trajetória curva, sua aceleração será representada pelas componentes x e y como na geometria abaixo.

α B = A C +   A B / C

α B =   4   +   ( 3 2 0,5 ] +   [ 8 0,5 ]

( α B ) X =   - 4 + 4,5 cos ⁡ 30 ° + 4   s e n   30 ° = 1,897   m / s 2 ( α B ) y =   0 + 04,5 s e n   30 ° - 4 cos ⁡ 30 ° =   - 1,214   m / s 2

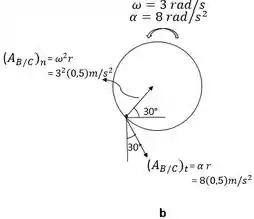
A sua intensidade poderá ser escrita da seguinte forma, relacionando as duas componentes X e Y :

α B = ( ( α B ) X ) 2 + ( ( α B ) Y ) 2  

α B =   ( 1,897 ) 2 + ( - 1,214 ) 2

α B =   2,25   m / s 2

Visto que seu raio de curvatura é desconhecido, podemos determina-lo:

θ = t a n - 1 1,214 1,897 =   32,6 °

Passo 3

Outra forma de achar as incógnitas é:

α B = α C + α ×     r B / C   -   ω 2 r B / C  

( α B ) X = i + ( A B ) y j

=   - 4 i + 8 k ( - 0,5 cos ⁡ 30 °   i - 0,5   s e n   30 °   j ) - ( 3 ) 2 ( - 0,5 cos ⁡ 30 °   i - 0,5   s e n   30 ° j )

( α B ) y = 0   –   8 ( 0,5 cos ⁡ 30 ° ) + 3 2 0,5   s e n   30 ° =   - 1,214   m / s 2

α B =   1,897 2 + - 1,214 2 =   2,25   m / s 2

θ = t a n - 1 1,214 1,897   = 32,6 °

Resposta

α B =   2,25   m / s 2

θ =   32,6 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As duas hélices com 800 mm de raio giram no sentido anti-horário com uma velocidade angular constante ω = θ ˙ = 2r a d / s em torno do eixo em O montado em um bloco deslizante. A aceleração do bloco é
15.222. A placa circular mostrada na figura gira em torno de seu diâmetro vertical a uma taxa constante 1 10 rad /s. Sabendo que na posição mostrada o disco se encontra no plano XY e o ponto D da alça
15.220. A barra AB está soldada em uma placa de 300 mm de raio que gira com uma taxa constante 1 6 rad /s. Sabendo que o colar D se desloca na direção da extremidade B da barra a uma velocidade consta
15.221. A barra dobrada mostrada na figura gira à taxa constante 1 3 rad /s. Sabendo que o colar C se desloca na direção do ponto D com uma velocidade relativa constante u 1 m/s, determine, para a pos