Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 123

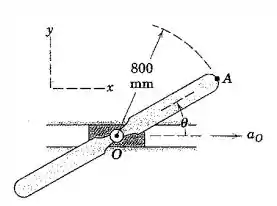
As duas hélices com 800 mm de raio giram no sentido anti-horário com uma velocidade angular constante ω = θ ˙ = 2   r a d / s em torno do eixo em O montado em um bloco deslizante. A aceleração do bloco é a O = 3   m / s 2 . Determine o módulo da aceleração da extremidade A da pá quando (a) θ = 0 , (b)   θ = 90 ° e (c)   θ = 180 ° . A velocidade de O ou o sentido de ω afetam os cálculos?

Passo 1

Nesta questão, podemos observar que existe movimento relativo entre os pontos O e A, pois a hélice gira em torno de O, que se desloca na horizontal. Bom, a princípio, já estamos feras em velocidade relativa, muito estudada na Seção 5.4.

PORÉM, existe um PLUS neste exercício (na verdade, nesta seção): a aceleração. A equação da aceleração relativa é similar a da velocidade relativa.

a A = a O + a A / O

Mas o termo a A / O pode ser escrito como:

a A = a O + ( a A / O ) n + ( a A / O ) t

Onde:

( a A / O ) n = ω × ( ω × r A O ) → é a aceleração relativa normal e ela aponta para o centro O.

( a A / O ) t = α × r A O → é a aceleração relativa tangencial e ela é perpendicular à distancia AO.

Representando os vetores na Figura, temos:

Bom, depois dessa breve revisão, podemos iniciar a desenvolver a questão.

Como não há aceleração angular α = 0 , o termo   ( a A / O )   t = 0 .

Ah, a questão pede apenas o módulo, então não vamos nos preocupar com notação vetorial.

Passo 2

  1. Nesta condição: θ = 0

    2. Representando o diagrama de vetores:

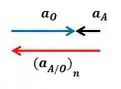
    Da equação: a A = a O + ( a A / O ) n

    a A = 3 - 2 × 2 × 0,8 = - 0,2   m / s 2

    Passo 3

  2. Nesta condição, θ = 90 °

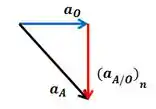
    3. Podemos resolver por Pitágoras:

    a A 2 = a O 2 + ( ( a A O ) n ) 2   =   3 2 + 3,2 2

    a A = 4,39   m / s 2

    Passo 3

  3. Nesta condição, θ = 180 °

a A = 3 + 2 × 2 × 0,8 = 6,2   m / s 2

Resposta

  1. a A = - 0,2   m / s 2

  2. a A = 4,39   m / s 2

  3. a A = 6,2   m / s 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Com referencia às hélices e o bloco deslizante do mancal do Prob. 5/123 onde a O = 3 m / s 2 . Se θ ¨ = 5 r a d / s 2 e θ ˙ = 0 quandoθ = 0 , encontre a aceleração do ponto A para esse instante.
Um recipiente para resíduos é descarregado pelo mecanismo ativado hidraulicamente. Se a haste do pistão parte do repouso na posição indicada e possui uma aceleração de 0,5 m/s² no sentido mostrado, ca
Determine a aceleração do ponto B no equador da Terra, reapresentado aqui a partir do Prob. 5/64. Utilize os dados Fornecidos naquele problema e assuma que a trajetória orbital da Terra é circular, co
O centro O do disco possui a velocidade e a aceleração indicadas na figura. Se o disco rola sem deslizar sobre a superfície horizontal, determine a velocidade de A e a aceleração de B para o instante
Um carro possui uma aceleração para frente a = 4 m / s 2 sem deslizar seus pneus de 600 mm de diâmetro. Determine a velocidade v do carro quando um ponto P sobre o pneu na posição indicada terá a comp