Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 99

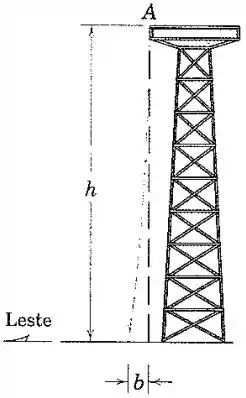
Um objeto que é liberado a partir do repouso do topo A de uma torre de altura h parecerá não cair em linha reta devido ao efeito da rotação da Terra. Pode ser demonstrado que o objeto tem uma aceleração horizontal para o leste em relação à superfície horizontal da Terra igual a 2 v y ω cos ⁡ γ , onde v y é a velocidade de queda livre, ω é a velocidade angular da Terra, e γ é a latitude, norte ou sul. Determine o desvio b se h = 300   m e γ = 30 ° norte. Da Tabela D/3, ω = 0,7292 10 - 4   r a d / s e da Fig. 1/1, g = 9,793   m / s 2 .

Passo 1

Galera, na queda livre, teremos:

v y = v 0 y - g t

v y = - g t

Então a aceleração horizontal será:

a x = 2 v y ω cos ⁡ γ = 2 - g t ω cos ⁡ γ

a x = - 2 g ω cos ⁡ γ   t

Se integrarmos essa equação, obtemos:

v x = - 2 g ω cos ⁡ γ t 2 2

Integrando novamente:

x = - 2 g ω cos ⁡ γ t 3 6

Passo 2

Agora que temos a equação do deslocamento em função do tempo, obteremos x = - b se t = t q , onde t q é o tempo total da queda. Mas isso podemos calcular usando a seguinte equação:

y = y 0 + v 0 y t - 1 2 g t 2

0 = h + 0 - 1 2 g t q 2

t q = 2 h g

Passo 3

Agora fazemos x = - b e t = t q na equação obtida no P a s s o   1 :

x = - 2 g ω cos ⁡ γ t 3 6

- b = - 1 6 2 g ω cos ⁡ γ 2 h g 3

b = 1 3 g ω cos ⁡ γ 2 h g 3 / 2

Se substituirmos h = 300   m , γ = 30 ° , ω = 0,7292 10 - 4   r a d / s e g = 9,793   m / s 2 , obteremos:

b = 0,0989   m

b = 98,9   m m

Resposta

b = 98,9   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

38. Quando um corpo é projetado para uma alta altitude acima da superfície da terra, a variação da aceleração da gravidade com respeito à altitude y deve ser levada em consideração. Desprezando a resi
25. Quando uma partícula é projetada verticalmente para cima com uma velocidade inicial de v 0 , ela experimenta uma aceleração a = - g + k v 2 , onde g é a aceleração devida à gravidade; k é uma cons
Uma bola é chutada do ponto A com a velocidade inicial v a = 10 m/s. Determine o alcance R e a velocidade escalar quando a bola tocar o solo.
Uma bola de futebol americano deve ser chutada sobre o poste do gol que fica a 4,5 m de altura. Se a sua velocidade escalar inicial é v A = 24m / s , determine se ela consegue ultrapassar o poste do g
Pacotes pequenos movendo-se sobre uma esteira transportadora caem dentro de um carrinho de carga de 1 m de comprimento. Se a esteira está se movendo com uma velocidade escalar constante de v c = 2m /