Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 73

Uma pequena conta de massa m é conduzida por um aro circular de raio r que gira em torno de um eixo vertical fixo. Mostre como se pode determinar a velocidade angular ω do aro pela observação do ângulo θ que localiza a conta. Despreze o atrito em sua análise, mas assuma que uma pequena quantidade de atrito está presente para amortecer qualquer movimento da conta em relação ao aro uma vez que uma velocidade angular constante tenha sido estabelecida. Aponte quaisquer restrições sobre sua solução.

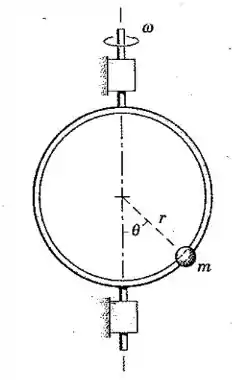
Passo 1

Vamos desenhar as forças envolvidas:

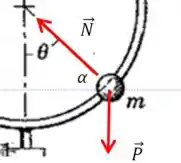
Lembre-se de que nosso verdadeiro interesse é achar a velocidade angular ω . Bom, essa velocidade angular está associado a um movimento circular, certo?

Então podemos ter certeza de que existe uma força centrípeta mantendo esse movimento, e de que essa força aponta para o centro da trajetória!

Mas tome cuidado: a trajetória circular associada à ω não é o aro, é um círculo como esse, que se move para cima e para baixo conforme a bola percorre o arco:

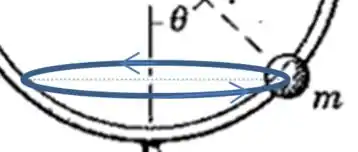
E a força que aponta para o centro desse círculo é:

F C = N sen ⁡ θ = m r ' ω 2

Onde r ' é o raio da trajetória circular. Observando a figura podemos ver que:

r ' = r sen ⁡ θ

Então:

N sen ⁡ θ = m r sen ⁡ θ   ω 2

N = m r ω 2

Passo 2

Ok, o que mais podemos afirmar pelo diagrama de forças? A componente vertical da força normal tem que se anular com o peso:

N y = P

N cos ⁡ θ = m g

N = m g cos ⁡ θ

Juntando esse resultado com a expressão de cima, podemos escrever o seguinte:

m g cos ⁡ θ = m r ω 2

ω = g r cos ⁡ θ

Beleza, essa é a expressão para a velocidade angular do aro.

Passo 3

A questão também pede para identificarmos as restrições desse nosso resultado. Bem, ao longo da nossa resolução, a gente simplesmente assumiu que ω era suficiente para gerar os movimentos circulares da bola.

Tomando isso como verdadeiro, chegamos nessa expressão aqui:

ω = g r cos ⁡ θ

cos ⁡ θ = g r ω 2

Nessa expressão está implícita a exigência para que esses movimentos possam ocorrer!

cos ⁡ θ ≤ 1

ω 2 ≥ g r

Ou seja, se a velocidade angular não atendesse a essa restrição, nem sequer haveria o movimento que nós analisamos.

Resposta

A velocidade angular é ω = g r cos ⁡ θ , e uma condição para que o movimento ocorra é ω 2 ≥ g / r .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O carro tem uma velocidade de 70k m / h na base da depressão quando o piloto aciona os freios, provocando uma desaceleração de 0,5g . Qual é o ângulo θ mínimo da almofada do banco para o qual um pacot
O braço ranhurado gira no plano horizontal em torno do eixo vertical fixo que passa pelo ponto O . O cursor C de 2k g é puxado em direção a O na taxa constante de 50m m / s tracionando o cordão S . No
O tambor com diâmetro de 650m m gira em torno de um eixo horizontal com uma velocidade angular constante Ω = 7,5r a d / s . O pequeno bloco A não possui movimento em relação à superfície do tambor qua
O tambor rotativo de uma secadora de roupa é mostrado na figura. Determine a velocidade angular Ω do tambor que resulta na perda do contato entre as roupas e o tambor em θ = 50 ° . Assuma que as peque
O pequeno cursor A de 180g se desloca sem atrito considerável no tubo vazado, que gira em um plano horizontal com uma velocidade constante Ω = 7r a d / s . O cursor é lançado com uma velocidade inicia