Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 110
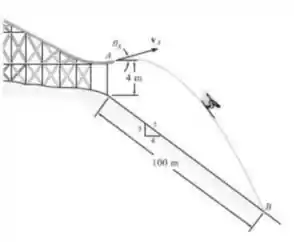
Observou-se que o esquiador deixa a rampa A formando um ângulo com a horizontal. Se ele atinge o solo em B, determine sua velocidade escalar inicial e o tempo de voo .
Passo 1
Precisamos trabalhar com plano inclinado! Vamos começar determinando as distâncias percorridas pelo nosso esquiador, tanto no eixo quanto no . Começando pelo primeiro, que é mais fácil, temos:
E em relação a , temos:
Certo??? Errado!!! Muito cuidado nesta hora!! O nosso esquiador começa saltando do ponto A, da nossa rampa. Esta rampa está a uma altura de do solo. Temos que somar então este comprimento a nossa distância , portanto, a verdadeira distância percorrida no sentido de é:
Agora, só nos basta aplicarmos as equações da cinemática para resolvermos o nosso problema!
Passo 2
Vamos começar utilizando as relações na direção do eixo . Neste sentido, o esquiador não está sujeito a nenhuma aceleração. Além disto, decompondo a sua velocidade neste sentido, obtemos:
Aplicando esta relação na equação da cinemática, obtemos:
Como obtemos uma relação entre e , precisamos de outra para podermos determinar seus valores!
Passo 3
Como obteremos uma nova relação? Se nós já trabalhamos com o eixo , nos falta o eixo , correto? É esperado que, ao trabalharmos com as equações envolvendo este eixo, vamos obter a relação que desejamos. Além de esperado, é o que realmente acontecerá!!! Vejamos abaixo!
Como na direção do eixo o nosso esquiador está sob ação da gravidade e a sua velocidade é dada por , temos a seguinte equação:
Cuidado com o sinal de . Como ele está abaixo da nossa origem (ponto A), o seu valor é negativo. Vamos substituir a relação entre e descoberta no passo anterior. Temos:
E calculando o valor de , temos: