Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 83
Onde atua a resultante das duas forças?
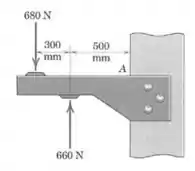
Passo 1
Vamos começar calculando o vetor para a força resultante. Como todas as forças têm a mesma direção, a soma vetorial fica bem simples:
E então a resultante é:
Passo 2
Agora queremos determinar a posição em que essa força atua. A posição não altera a força resultante, mas altera o momento resultante.
A ideia aqui é que a nossa força atue em um ponto onde o momento resultante seja o mesmo do estado inicial. Vamos calcular esse momento:
E o sinal negativo apareceu na força de porque ela favorece a rotação no sentido horário.
Para que a nossa força produza o mesmo momento precisamos garantir a seguinte igualdade:
A força tem um sinal negativo porque aponta de cima para baixo, o que está de acordo com o fato de que , o que indica rotação no sentido anti-horário.
Resposta
A força atua à esquerda do ponto .