Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.8 - Ex. 203

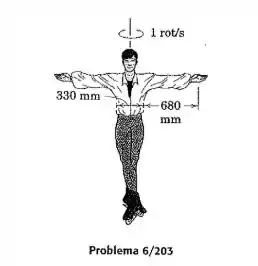
O patinador no gelo de 74   k g com braços esticados horizontalmente gira em torno de um eixo vertical com uma velocidade de rotação de 1   r o t / s . Estime a sua velocidade de rotação N se ele retrai totalmente os seus braços, trazendo as suas mãos para muito perto da linha de centro de seu corpo. Como uma aproximação aceitável, modele os braços esticados como barras esbeltas uniformes, cada uma com 680   m m de comprimento, com uma massa de 7   k g . Modele o tronco como um cilíndrico maciço de 60   k g com 330   m m de diâmetro. Considere o homem com os braços retraídos como um cilindro maciço de 74   k g com 330   m m de diâmetro. Despreze o atrito na interface do gelo e os patins.

Passo 1

Conforme sugerido no enunciado, os braços esticados podem ser modelados como barras esbeltas uniformes, assim conseguiremos calcular o momento de inércia de massa.

Agora resta aplicar a equação da consevação da quantidade de movimento angular.

Passo 2

H 1 = H 2

Substituindo os dados do problema, temos

1 2 60 0,33 2 2 + 2 1 12 7 0,68 2 + 7 0,68 + 0,3 2 2 × 1 = 1 2 74 0,33 2 2 × N

Simplificando e resolvendo para N , obtemos

N = 4,89   r o t / s

Resposta

N = 4,89   r o t / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os coeficientes de atrito entre a carga e o reboque de piso plano mostrado na figura são μ s = 0,40 e μ k = 0,30. Sabendo que velocidade escalar do equipamento é 72 km/h, determine (a) a menor distânc
A aceleração de um pacote deslizando no ponto A é 3 m/s2. Considerando que o coeficiente de atrito cinético é o mesmo em cada seção, determine a aceleração do pacote no ponto B.
Se a distância de frenagem de um automóvel a 96 km/h é de 45 m em um piso nivelado, determine a distância de frenagem desse automóvel a 96 km/h quando ele está (a) subindo um plano inclinado de 5° e (
Determine a velocidade escalar teórica máxima que um automóvel partindo do repouso pode atingir após ter percorrido 400 m. Assuma que o coeficiente de atrito estático é de 0,80 entre os pneus e o pavi
Os dois blocos mostrados na figura estão originalmente em repouso. Desprezando as massas das roldanas e o efeito do atrito nessas roldanas e considerando que os coeficientes de atrito entre ambos o bl