Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.8 - Ex. 205
A barra esbelta de massa e comprimento é liberada a partir do repouso na posição horizontal mostrada. Se o ponto da barra se prende na articulação em após o impacto, determine a velocidade angular da barra imediatamente após o impacto em termos da distância . Calcule o valor da sua expressão para e .
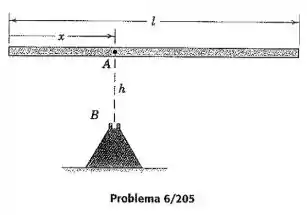
Passo 1
Para a queda livre da barra podemos aplicar o princípio da conservação da energia mecânica, de onde tiramos que
Simplificando e resolvendo para , obtemos a velocidade com que o ponto na barra colide com a articulação em .
Passo 2
Pela conservação da quantidade de movimento angular, temos
Simplificando, ficamos com
Resolvendo para , obtemos
Passo 3
Caso 1:
Caso 2:
Caso 3:
Resposta
Exercícios de Livros Relacionados
O bloco A tem a massa de 40 kg e o bloco B tem a massa de 8 kg. Os coeficientes de atrito entre todas as superfícies de contato são μ s = 0,20 e μ k = 0,15. Se P = 0, determine (a) a aceleração do blo
Duas esferas idênticas A e B, cada uma com massa m, estão conectadas por uma corda inextensível e não elástica de comprimento L, e em repouso a uma distância a uma da outra sobre uma superfície horizo
Em um cruzamento, o carro B ia para o sul e o carro A viajava 30° para nordeste, quando se envolveram em uma colisão. Pela investigação, soube-se que, após a batida, os dois carros se engataram e derr
Um vagão ferroviário de 20 Mg movendo a 4 km/h é acoplado a um vagão ferroviário de 40 Mg que está em repouso com as rodas travadas ( μ k = 0,30 ). Determine (a) a velocidade dos carros depois que aco
Dois nadadores A e B, com massas de 76 kg e 50 kg, respectivamente, estão em cantos diagonalmente opostos de um flutuador quando percebem que o flutuador se soltou de seu ancoradouro. O nadador A imed