Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 31
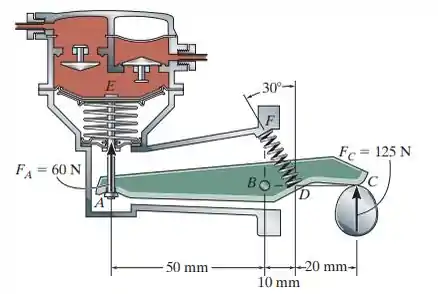
A operação da bomba de combustível de um automóvel depende da ação basculante do balancim , que tem um pino em e sofre a ação de molas em e . Quando o came liso está na posição mostrada, determine as componentes horizontal e vertical da força no pino e a força ao longo da mola para que haja equilíbrio. A força vertical que atua sobre o balancim em é , e em é .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta é uma questão que pela geometria parece ser difícil. Entretanto, ao analisarmos com calma, vemos que não é isto tudo! Só o fato dos pontos , , e serem colineares, facilita tudo!
A questão nos pede para determinarmos as reações no pino ( e ) e a força na mola .
Como todo o balancim está em equilíbrio, basta lembrarmos que:
Então, vamos as contas!
Passo 2
Vamos começar determinando a força na mola . Assumindo o seu sentido para baixo, vamos realizar o somatório de momentos em relação ao ponto .
Desta forma, temos:
Passo 3
Agora nos resta determinarmos as reações no pino . Para isto, será necessário analisarmos o equilíbrio do balancim pelo somatório de forças.
Então fazendo o somatório de forças, tanto na direção quanto na direção , obtemos:
Resolvendo o sistema acima, obtemos e .
E assim finalizamos a questão!