Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.3 - Ex. 27
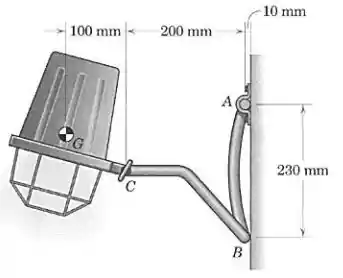
A luminária de parede de tem seu centro de massa em . Determine as reações em e e também calcule o momento suportado pelo parafuso de ajuste em . (Note que a estrutura leve tem cerca de de tubo, orientado para dentro e para fora do papel, tanto em quanto em .)
Passo 1
A soma dos momentos em torno de deve se anular, ou seja:
Passo 2
Temos equilíbrio de forças na horizontal, então:
E na vertical também:
Passo 3
Por último, realizamos a soma de todos os momentos em torno de e igualamos a zero, a fim de obter o momento suportado pelo parafuso de ajuste em :
Resposta
(sentido horário)
Exercícios de Livros Relacionados
Um determinado comprimento de um cabo de transmissão está suspenso das duas torres, como mostrado. O cabo tem uma massa de 20 kg por metro. Se a máxima força trativa admissível no cabo vale 75 kN, det
Um cilindro circular de massa específica ρ 1 flutua em um líquido de massa específica ρ 2 . Se d é o diâmetro do cilindro e h é a altura submersa, faça o gráfico da razão r = h / d em função de ρ 1 /
Determine as componentes vertical e horizontal da reação nos pinos A e C da estrutura de dois membros
Se uma força F=50 N age sobre a corda, determine a força de corte sobre o galho de árvore liso em D e as componentes horizontal e vertical da força atuando no pino A. A corda passa por uma pequena pol
O caminhão e o tanque possuem pesos de 40 kN e 100 kN respectivamente. Seus centros de gravidade respectivos são localizados nos pontos G1 e G2 . Se o caminhão está em repouso, determine as reações em