Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 71

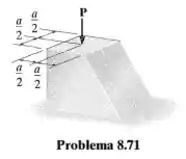
O apoio está sujeito à carga de compressão P. Determine as tensões normais absolutas máximas e mínimas que agem no material.

Passo 1

Como a força axial será constante   ( N - P = 0 ) no interior da peça, devemos descobrir onde o momento interno é máximo

Assim, por somatório de momento temos:   M a + x 2 - a 2 = 0                   M = 0,5 P x

Também podemos obter a área em função de x: A = a a + x e o momento de inércia I = a a + x 3 12

Obtemos então o diagrama de corpo livre em função de x

Passo 2

Agora substituímos os valores na equação de tensão:

σ C = - N A - M × C I = - P a a + x - 0,5 P x × 0,5 ( x + a ) a a + x 3 12 = - P a a + x - 3 P x a ( a + x ) 2

Esta função será máxima quando sua derivada for zero.

d d x - P a a + x - 3 P x a a + x 2 = 0

Neste caso x=0,5a

Substituindo esse valor em - P a a + x - 3 P x a ( a + x ) 2 temos σ m á x = 1,33 P a 2 ( C )

Passo 3

Agora para a mínima (ou máxima de tração) faremos o mesmo, porém com o sinal da flexão oposto.

σ C = - N A + M × C I = - P a a + x - 0,5 P x × 0,5 x + a a a + x 3 12 = - P a a + x + 3 P x a ( a + x ) 2

Igualando d d x - P a a + x + 3 P x a a + x 2 = 0

Temos x=2a

Substituindo esse valor em - P a a + x + 3 P x a ( a + x ) 2 temos σ m i n = P 3 a 2 ( T )

Resposta

σ m á x = 1,33 P a 2 ( C )

σ m i n = P 3 a 2 ( T )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A componente AB tem uma seção transversal retangular uniforme de 10×24m m . Para o carregamento mostrado, determine as tensões normal e de cisalhamento (a) no ponto H e (b) no ponto K.
Uma força de 13kN é aplicada a coluna ABD com 60mm de diâmetro de ferro fundido conforme mostrado. No ponto H, determine (a) as tensões principais e os planos principais, (b) a tensão de cisalhamento
Três forças são aplicadas a uma placa com 101,6mm de diâmetro que está fixada a um eixo cheio AB de 45,7 mm de diâmetro. No ponto H, determine (a) as tensões e os planos principais e (b) a tensão de c
O tubo de aço AB tem 100MM de diâmetro externo e parede com 8mm de espessura. Sabendo que a tensão no cabo é de 40kN, determine as tensões normal e de cisalhamento no ponto H.
Duas forças são aplicadas ao tubo AB, conforme mostra a figura. Sabendo que o tubo tem diâmetros interno e externo iguais a 35mm e 42 mm, respectivamente, determine as tensões normal e de cisalhamento