Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 86
O parafuso de olhal é usado para sustentar a carga de . Determine seu diâmetro com aproximação de múltiplos e a espessura exigida com aproximação de múltiplos de do suporte de modo que a arruela não penetre ou cisalhe o suporte. A tensão normal admissível para o parafuso é e a tensão de cisalhamento admissível para o material do suporte é .
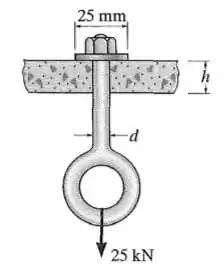
Passo 1
Oláaaa, querido! Tá bem?
Ele quer saber as dimensões da nossa estrutura para ela aguentar a carga de sem dar nenhum problema.
Primeiro, ele fala sobre o parafuso. Ele diz que ele aguenta de tensão normal e precisa suportar a carga de . Aí ele quer saber o diâmetro desse parafuso.
E depois ele fala sobre o suporte. Ele não pode ser penetrado pela arruela (essa coisinha em volta do parafuso). A gente quer saber a espessura desse suporte sabendo que a tensão de cisalhamento que ele aguenta é .
Cara, a ideia aqui é usar essas informações e a expressão de tensões admissíveis para achar as dimensões do suporte e do parafuso.
Bora ver como fazer essa!
Passo 2
Vamos começar pelo parafuso.
Devemos lembrar que a tensão normal admissível é calculada da mesma forma que a tensão normal média, assim teremos
Mas como nosso parafuso tem área circular:
Ou seja, isso é a expressão do diâmetro do parafuso em função da força normal que ele suporta e sua tensão admissível.
Passo 3
Pela figura, vemos que a única força na direção normal da seção transversal do parafuso é a carga de . Então essa vai ser a força normal interna
Substituindo isso a tensão admissível normal do parafuso na nossa expressão do diâmetro, a gente vai achar
Arredondando para múltiplo de 5 vamos obter .
Passo 4
Agora vamos pensar sobre o suporte. A tensão de cisalhamento tem essa expressão:
Sendo que é a força paralela à seção que pode sofrer cisalhamento e é a área dessa seção.
O que acontece aqui é que o parafuso vai tender a descer por causa da carga de . Mas a arruela não vai deixar, ela vai prender ele ao suporte. E isso faz com o que o suporte receba uma força de paralela a sua seção transversal.
E essa força é exercida pela borda da arruela, então a seção do suporte que sofre essa carga é uma seção da altura do suporte, mas de comprimento igual ao comprimento da borda da arruela. Algo assim:
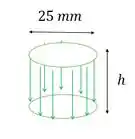
Para visualizar isso você pode pensar assim: se a arruela afundar no suporte (se o suporte não resistir ao cisalhamento), o suporte vai ficar com um buraco. A área lateral desse buraco vai ser a altura do suporte vezes o comprimento da borda da arruela que vale , certo?
Então essa é nossa área e vale
Percebe que é o mesmo que .
Passo 5
Então nossa expressão da tensão fica
Isolando quem a gente quer achar:
Cara, é a carga paralela a essa seção. Ou seja, é uma carga vertical. Então podemos dizer que , a carga que a arruela transmite para o suporte ao longo da nossa seção .
Agora, resta-nos substituir os valores e obteremos
Também aproximando para múltiplo de 5 vamos obter