Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 2.Problemas - Ex. 10
O cabo AB não está esticado quando θ = 45º. Se uma carga vertical for aplicada à barra AC e provocar a mudança do ângulo para θ = 47º, determine a deformação normal no cabo.
Passo 1
Olá, querido! Cê tá bem? Então, ele quer saber a deformação normal de se uma carga for aplicada e mudar o ângulo para .
A fórmulinha da deformação normal é
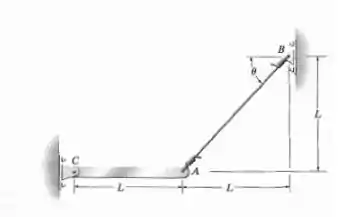
Onde é o comprimento inicial do cabo . Percebe que temos um triângulo retângulo ali na figura:
Então a gente pode achar esse usando PItagoras:
Aí falta a achar o comprimento do cabo depois da deformação, que a gente chamou de . A carga aplicada faz esse cabo aumentar, e por isso o ângulo muda. Aí a gente precisa achar o comprimento de depois dessa mudança para poder achar . Bora lá!
Passo 2
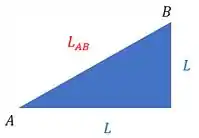
Então, antes da deformação, a nossa estrutura tinha essa cara:
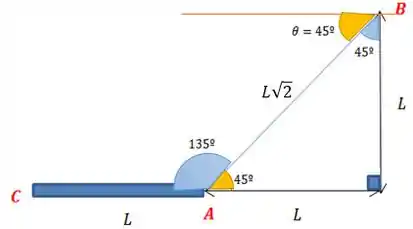
Dela a gente pode tirar esse triâgulo:
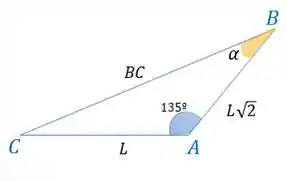
Usando a famosa Lei dos Cossenos, podemos achar o valor do lado :
Podemos também descobrir o ângulo do vértice B, também pela lei dos cossenos:
Passo 3
E para que a gente achou essas coisas? Porque a gente quer o comprimento de depois que o ângulo muda, então é importante achar algumas medidas da nossa estrutura para o original.
Antes da deformação, nós temos a seguinte situação ali naquele triâgulo que a gente destacou:
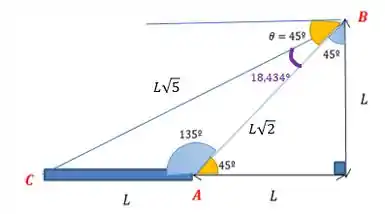
Com a deformação, o ângulo que faz com a horizontal, passa de para e aumenta. Repara o que acontece
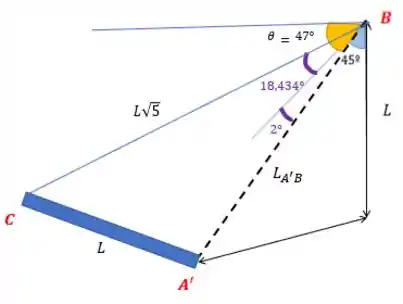
Percebe que o segmento não muda de posição, porque os pontos e são fixos. E não muda de tamanho porque essa é uma barra rígida.
Então quando aumenta , o ângulo de vai para para , já que permanece na mesma orientação.
Passo 4
Aí dessa útima figura, podemos tirar esse triângulo:
Usando lei dos cossenos, podemos calcular o tamanho de BA’, que é o valor de depois da deformação
Chegamos, portanto, em uma equação de segundo grau... resolvendo ela, vamos ter:
Passo 5
Como temos e , podemos calcular a deformação: