Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 2.Problemas - Ex. 13
A forma original de uma peça de plástico é retangular. Determine a deformação por cisalhamento nos cantos D e C se o plástico se distorce como mostram as linhas tracejadas.
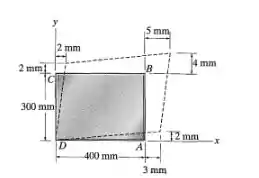
D e C se o plástico se distorcer como mostram as linhas tracejad
Passo 1
Primeiramente, vamos nomear alguns ângulos e representar as deformações:
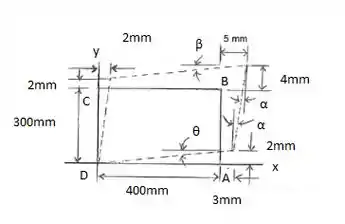
Como esses ângulos são muito pequens, valem as simplificações Logo:
Passo 2
Com isso, podemos calcular as deformações por cisalhamento:
-3 rad
-3 rad
Resposta
-3 rad
-3 rad
Exercícios de Livros Relacionados
12. Um extensômetro está montado no eixo de aço A - 36 de 25m m de diâmetro como mostra a figura. Quando o eixo está girando a uma velocidade angular ω = 1760r e v / m i n e usando um anel corrediço,
13. As componentes do estado plano de deformação no ponto sobre a chave de porca são ϵ x = ( 350 × 10 - 6 ) , ϵ y = ( 400 × 10 - 6 ) e γ x y = ( - 675 × 10 - 6 ). Use as equações de transformação da d
Estime o aumento no volume do taque do Problema 10.59 . Dica: Use os resultados do Problema 10.54 como confirmação.
Um vaso de pressão esférico de parede fina com raio interno r e espessura t é submetido a uma pressão interna p . Mostre que o aumento de volume no interior do vaso é Δ V=( 2 p π r 4/ E t ) ( 1- v) .
As extremidades do vaso de pressão cilíndrico são fechadas com tampas semiesféricas para reduzir a tensão de flexão que ocorreria se as tampas fossem planas. As tensões de flexão nas linhas de junção