Enunciado
Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 2.Problemas - Ex. 52
Uma partícula de massa m se movimentando em uma dimensão tem energia potencial U(x) = U0[2(x/a)2 – (x/a)4], onde U0 e a são constantes positivas.
- Determine a força F(x) atuando sobre a partícula.
- Faça um gráfico de U(x). Determine as posições de equilíbrio estável e instável.
- Qual será a frequência angular das oscilações em torno do ponto de equilíbrio?
- Qual será a velocidade mínima que a partícula deverá ter na origem para escapar para o infinito?
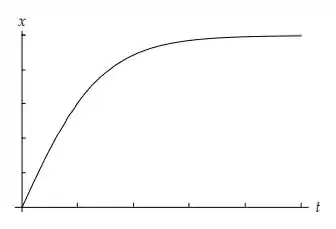
- Em t = 0, a partícula encontra-se na origem e sua velocidade é positiva e igual em magnitude à velocidade do item (d). Determine x(t) e faça um gráfico do resultado.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de mecânica Newtoniana.
Item a
A partir do que o enunciado nos forneceu teremos:
Passo 2
Item b
O gráfico de U(x):
Quando F = 0, há equilíbrio; além disso, quando U tem um mínimo local (ou seja, dF/dx 0) é instável.
Assim, pode-se ver que neste problema x = a e x = –a são posições de equilíbrio instáveis, e x = 0 é uma posição de equilíbrio estável.
Passo 3
Item c
Em torno da origem temos que:
Como a frequência é dada por:
Temos que:
Passo 4
Item d
Para escapar para o infinito de x = 0, a partícula precisa chegar pelo menos ao pico do potencial:
Passo 5
Item e
Pela conservação de energia temos:
Notamos que, no caso ideal, como a velocidade inicial é a velocidade de escape encontrada em d), idealmente x é sempre menor ou igual a constante a, então da expressão acima:
O gráfico é apresentado a seguir:
Resposta
Ver passo a passo.