Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 2.Problemas - Ex. 50

De acordo com a relatividade especial, uma partícula de massa m0 em repouso, acelerada em uma dimensão por uma força F, obedece a equação de movimento dp/dt = F. Nesse caso, p = m0v/(1 – v2/c2) é a quantidade de movimento relativístico, que se reduz a m0v para v2/c2

  1. Para o caso de F constante e condições iniciais x(0) = 0 = v(0), determine x(t) e v(t).
  2. Faça um gráfico do seu resultado para v(t).
  3. Suponha que F/m0 = 10 m/s2 ( ≈ g na Terra). Qual será o tempo necessário para que a partícula alcance metade da velocidade da luz e 99% da velocidade da luz?

Passo 1

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de mecânica Newtoniana.

Item a

A partir do que o enunciado nos forneceu teremos:

F = d p d t = d d t m 0 v 1 - v 2 c 2 = > ∫ 0 t F d t = ∫ 0 t d m 0 v 1 - v 2 c 2 = > F t = m 0 v t 1 - v 2 t c 2

Isolando v(t) ao elevarmos ao quadrado a equação obtida:

F 2 t 2 = m 0 2 v 2 t 1 - v 2 t c 2 = > c 2 - v 2 t v 2 t c 2 = m 0 2 F 2 t 2 = > v - 2 - 1 c 2 = m 0 2 F 2 t 2 = > v - 2 = m 0 2 F 2 t 2 + 1 c 2

= > v t = 1 m 0 2 F 2 t 2 + 1 c 2 = c 2 F 2 t 2 m 0 2 + F 2 t 2 = F t m 0 2 + F 2 t 2 c 2

A partir da velocidade fazemos:

x t = ∫ 0 t v t d t = c 2 F m 0 2 + F 2 t 2 c 2 - m 0

Passo 2

Item b

O gráfico de v(t) é apresentado a seguir:

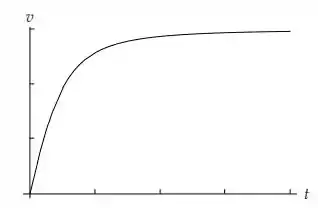
Passo 3

Item c

Do item a temos que:

t = v m 0 F 1 - v 2 c 2

Como foi dado que:

F m 0 = 10

Temos que:

  • Para v = c/2:

    • t = c 2 10 1 - c 2 2 c 2 = c 2 10 3 4 = c 10 3

    Que ao substituímos o valor de c (300 000 000 m/s) temos:

    t = 300000000 10 3 ≅ 1,732 ∙ 10 7   s   o u   200   d i a s   o u   0,55   a n o s

  • Para v = 0,99c:

t = 0,99 c 10 1 - 0,99 c 2 c 2 = 0,99 c 10 0,0199 ≅ 0,7018 c

Que ao substituímos o valor de c (300 000 000 m/s) temos:

t ≅ 0,7018 ∙ 300000000 ≅ 2,1054 ∙ 10 8   s   o u   2 436,8   d i a s   o u   6 , 67   a n o s

Resposta

Ver passo a passo.

Exercícios de Livros Relacionados

Quanta energia por quilograma deve ser fornecida a um satélite a fim de colocá-lo em uma órbita circular a uma altitude de ( a ) 600 k m e ( b )6.000k m ?
Uma sonda espacial descreve uma órbita circular de raio nR com velocidade v0 em torno de uma planeta de raio R e centro O. Mostre que (a) para que a sonda espacial deixar sua órbita e atingir o planet
Usando as respostas obtidas no Problema 13.107, mostre que a órbita circular pretendida e a órbita elíptica resultante interceptam-se nas extremidades do eixo menor da órbita elíptica.
Escreva os critérios para determinar se um equilíbrio é estável ou instável quando todas as derivadas até a ordem n, (d2U/dx2)0 = 0.
Duas estrelas ligadas gravitacionalmente com massas iguais m, separadas por uma distância d, giram ao redor do seu centro de massa em órbitas circulares. Demonstre que o período τ é proporcional a d3/