Enunciado
Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 2.Problemas - Ex. 7
Inclua a resistência do ar para os fardos de feno no problema anterior. Um fardo de feno tem massa aproximada de e área de cerca de . Considere a resistência do ar proporcional ao quadrado da velocidade e faça . Faça um gráfico das trajetórias no computador se os fardos de feno aterrissarem atrás dos animais. Para os casos com e sem resistência do ar. Se os fardos de feno fossem lançados ao mesmo tempo nos dois casos, qual seria a distância entre suas posições de aterrissagem?
Passo 1
E aí galera, vamos iniciar mais uma questão do nosso livro!
Bem galerinha, primeiramente temos que a expressão de Prandtl para a resistência do ar é dada por:
Onde é o coeficiente de arrasto adimensional, é a densidade do ar, é a velocidade e é a área da seção transversal do objeto medida perpendicularmente à velocidade. A força está sempre na direção oposta da velocidade, então tem a direção do vetor unitário , isso é:
Mas:
Então:
Podemos assim, dividir as forças em duas partes, sendo nas direções e como:
Agora definimos a força total no projetil igual a , como:
Podemos dividir a força em duas partes, obtendo:
Passo 2
Continuando, temos que a força resultante na direção é igual à força de resistência do ar, e a força resultante na direção é igual à força da gravidade subtraída da força de resistência do ar na direção , ou seja:
Substituindo os valores de e , temos:
Reorganizando as equações como:
Onde . Agora precisamos traçar essas funções, com condições iniciais de , , e . O procedimento será o seguinte:
- Encontre a velocidade para os valores iniciais
- A partir desta velocidade podemos encontrar a próxima velocidade.
- Multiplicando a aceleração por um pequeno intervalo de tempo
- Finalmente multiplicamos as velocidades e por e adicione-o à posição anterior.
Utilizando um software em python para fazer isso e o código é ilustrado na imagem a seguir:
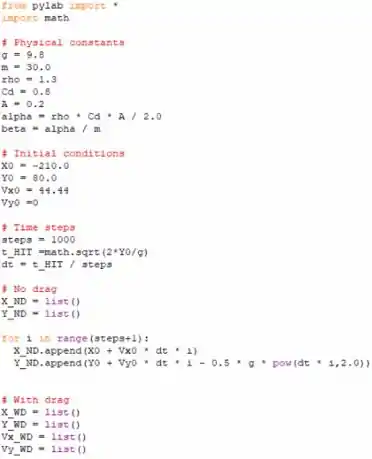
Passo 3
Em seguida plotamos o gráfico resultante do código:
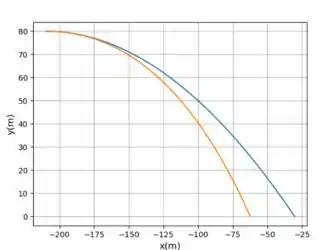
O laranja está com a resistência do ar, e o azul está sem. A distância entre eles em é:
Finalizamos aqui nossa questão, tudo beleza? Te vejo na próxima!