Enunciado
Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 2.Problemas - Ex. 24
Um esquiador pesando parte do repouso para descer uma encosta com inclinação de . Ele desliza encosta abaixo e, a seguir interrompe a impulsão ao longo de de neve nivelada até parar. Determine o coeficiente de atrito cinético entre os esquis e a neve. Qual velocidade o esquiador deverá alcançar na base da encosta?
Passo 1
E aí galera, vamos iniciar mais uma questão do nosso livro!
Primeiramente vamos anotar alguns dados importantes fornecido na questão:
Como na figura a seguir, o problema foi dividido em duas partes. Primeiro quando o esquiador está descendo a colina e segundo quando ele desce até parar.
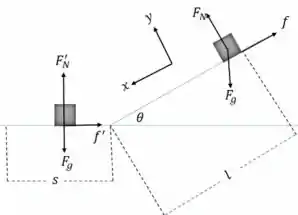
Então, no primeiro caso temos o peso do esquiador, a força normal sobre ele e a força de atrito. As equações do movimento.
Na direção temos:
E na direção , temos:
Desde,
Dessa forma, a aceleração é dada por:
Podemos ver que a aceleração é constante.
Agora para o segundo caso, as equações de movimento na direção e na direção são dadas respectivamente por:
Assim a gente pode expressar a aceleração na seguinte maneira:
E essa aceleração também será constante.
Passo 2
Portanto, como as acelerações são constantes podemos simplesmente encontrar a velocidade e a posição por integração simples como segue abaixo:
Então:
E:
Substituindo por , teremos:
Assim, se considerarmos que o ponto inicial e final é o início e o fim do morro, obtemos:
Onde é a velocidade final no morro. E se considerarmos que o ponto inicial e final está descendo o morro e onde ele parou, temos:
Passo 3
Agora, igualando as equações e , temos:
E substituindo pelos valores de e , calculados anteriormente, obtemos:
E a velocidade é:
Finalizamos aqui nossa questão, tudo beleza? Te vejo na próxima!