Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 63

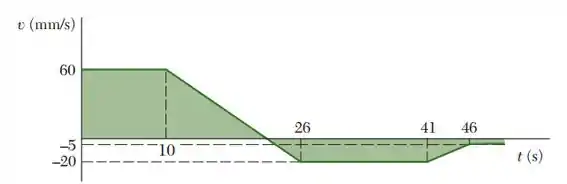
Uma partícula se move em uma linha reta com a velocidade mostrada na figura. Sabendo que x =   - 540 mm em t = 0: (a) construa as curvas a-t e x-t para 0 < t < 50 s e determine (b) a distância total percorrida pela partícula quando t = 50 s e (c) os dois instantes em que x = 0.

Passo 1

E ai gurizada tudo belezinha???

(a) a 1 = d e c l i v e de v-t curva no tempo t:

De t = 0       p a r a   t = 10 s v = c o n s t a n t e   ⇒ a = 0

  t = 10 s       p a r a   t = 26 s : a = - 20 - 60 26 - 10 =   - 5   m / s ²

  t = 26 s       p a r a   t = 41 s : v = c o n s t a n t e   ⇒ a = 0  

  t = 41 s       p a r a   t = 46 s : a = - 5 - ( - 20 ) 46 - 41 =   3   m / s ²

t = 46 s : v = c o n s t a n t e   ⇒ a = 0

Passo 2

x 2 = x 1 + ( á r e a   s o b   v - t     c u r v a     d e     t 1   p a r a   t 2 )

Em t = 10 s : x 10 = - 540 + 10 60 + 60   m

A seguir encontre um horário no qual v=0. Usando triângulos semelhantes.

t v = 0 - 10 60 = 26 - 10 80 ou t v = 0 = 22 s

Em t = 22 s : x 22 = 60 + 1 2 12 60 = 420   m

t = 26 s : x 26 = 420 - 1 2 4 20 = 380   m

t = 41 s : x 41 = 380 - 15 20 = 80   m

t = 46 s : x 46 = 80 - 5 20 + 5 2 = 17.5   m

t = 50 s : x 50 = 17.5 - 4   5 = - 2.5   m

Passo 3

(b) De t = 0       p a r a     t = 22 s :             d i s t â n c i a   v i a j a d a = 420 - - 540 = 960   m

t = 22 s       p a r a     t = 50 s :       d i s t â n c i a   v i a j a d a = | - 2.5 - 420 | = 422.5   m

D i s t â n c i a   t o t a l   p e r c o r r i d a = 960 + 422.5 f t = 1382.5   m

Passo 4

(C) Usando triângulos semelhantes

Entre 0 e 10s: ( t x = 0 ) 1 = 0 540 =   10 600

Ou

Entre46s e 50s: ( t x = 0 ) 2 - 46 17.5 = 4 20

Resposta

a)

b) = 1383   m

c) ( t x = 0 ) 1 = 9.00   s ou ( t x = 0 ) 2 = 49.5 s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula inicialmente em repouso em x = 1 m é acelerada até que sua velocidade dobre de intensidade entre x = 2 mex = 8 m . Sabendo que a aceleração da partícula é definida pela relação a = kx[ x
Um pedaço de um equipamento eletrônico que está protegido pelo material de embalagem cai de modo que ele atinge o solo com uma velocidade de 4m / s . Depois do impacto, o equipamento experimenta uma a
Uma partícula inicia em repouso na origem e recebe uma aceleração a = k / ( x + 4 ) ² ², onde aex é uma constante. Sabendo que a velocidade da partícula é 4m / s quando x = 8m , determine (a) o valor
Baseado em observações experimentais, a aceleração de uma partícula é definida pela relação a = - ( 0,1 + s e nx / b ) , onde aex são expressos em m / s ² ² e m , respectivamente. Sabendo que b = 0,8
A aceleração devida à gravidade de uma partícula caindo em direção a Terra é a = - g R ² / r ² ² ², onde r é a distancia a partir do centro da Terra até a partícula, R é o raio da Terra e g é a aceler