Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 57

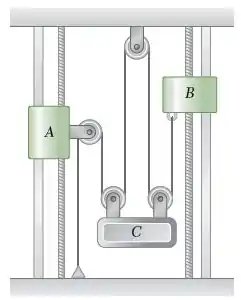
O colar A parte do repouso em t = 0 e se movimenta para baixo com uma aceleração constante de 140 m m / s ² . O colar B se movimenta para cima cm uma aceleração constante e sua velocidade inicial é de 160 m m / s . Sabendo que o colar B percorre 400 m m entre t = 0   e   t = 2 s , determine (a) a acelerações do colar B e do bloco C, (b) o instante em que a velocidade do bloco C é igual a zero e (c) a distancia que o bloco C terá percorrido naquele instante.

Passo 1

E ai galera tudo certinho? O enunciado pede que a gente encontre a acelerações do colar B e do bloco C, (b) o instante em que a velocidade do bloco C é igual a zero e (c) a distância que o bloco C terá percorrido naquele instante.

- y A + y C - y A + 2 y C + y C - y B = c o n s t a n t e

Então: - 2 v A - v B + 4 v C = 0

E - 2 a A - a B + 4 a C = 0

Dado: v A 0 = 0 a A = 140   m m / s ² ↓

v B 0 = 160   m / s ↑

a B = c o n s t a n t e ↑

Passo 2

Em t = 2 s y - y B 0 = 400   m m ↑

  1. Temos: y B = y B 0 + v B 0 t + 1 2 a B t ²

    2. Em t = 2 s :  

    - 400   m m . = ( - 160   m / s )   x   ( 2 s ) + 1 2 a B   x   ( 2 s ) ²

    a B = 160   m m . / s ²

    Passo 2

  2. Substituindo em Eq.(1) em t = 0

    3. - 2   x   0 - ( - 8 i n . / s ) + 4   x   v C 0 = 0 ou v C 0 = - 2 i n . / s

    Agora v C = v C 0 + a C t

    Quando v C = 0 :   0 = ( - 2 i n . / s ) + ( 3 i n . / s ² ) t

    Ou t = 2 3 s

  3. Temos: y C = y C 0 + v C 0 t + 1 2 a C t

Em t = 2 3 s : y C - y C 0 = ( - 2   m / s )   x   2 3 s + 1 2   x   ( 3   m . / s ² )   x   2 3 s 2

= - 0.667 m .

Resposta

  1. a B = 2 i n . / s ² ↑

    2. a C = 3 i n . / s ² ↓

  2. t = 0,667 s
  3. y C - y C 0 = 0,667 i n . ↑
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

27. Uma partícula move-se ao longo de uma linha reta com uma aceleração de a = 5 3 s 1 3 + s 5 2m / s 2 , onde sé é dado em metros. Determine a velocidade da partícula quando s = 2m, se ela partir do
34. Uma partícula move-se ao longo de uma linha reta com uma velocidade v = 200 sm m / s , onde s está indicado em mm. Determine a aceleração da partícula em s = 2000 mm. Quanto tempo leva para a part
30. A velocidade de uma partícula movendo-se ao longo de uma linha reta é v = v 0 - k s , onde k é constante. Se s = 0 quando t = 0, determine a posição e a aceleração da partícula como uma função do
37. A bola A é jogada verticalmente para cima com uma velocidade v 0 . A bola B é jogada para cima a partir do mesmo ponto com a mesma velocidade t segundos mais tarde. Determine o tempo decorrido t2
9. Uma partícula move-se ao longo de uma pista reta de tal maneira que sua posição é descrita pelo gráfico s-t. Construa o gráfico v –t para o mesmo intervalo de tempo.