Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 174

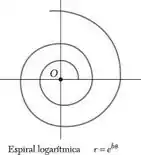
Uma partícula se move ao longo da espiral mostrada na figura. Determine a intensidade da velocidade da partícula em termos de b, θ , θ ˙ .

Passo 1

Fala aí galera tudo certinho? O enunciado pede que a gente determine a intensidade da velocidade da partícula em termos de b, θ , θ ˙ .

Consideramos a Espiral logarítmica.

r = e b θ

r ˙ = d r d t = b e b θ d θ d t = b e b θ θ ˙

Passo 2

As velocidads em relação ao raio e ao angulo sao dadas a seguir, equalizando-as temos as velocidade :D

v r = r ˙ = b e b θ θ ˙             v θ = r θ ˙ = e b θ   θ ˙

v = v r 2 + v θ 2 = e b θ θ ˙ b 2 + 1

Resposta

v = e b θ 1 + b 2   θ ˙

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O carro de corrida tipo Dragster parte do repouso e move-se ao longo de uma pista reta com uma aceleração – desaceleração descrita pelo gráfico. Construa o gráfico v-s para , e determine a distância p
A aceleração de uma lancha de corrida partindo do repouso é descrita pelo gráfico. Construa o gráfico v - s .
Uma motocicleta de corrida está se movendo ao longo de uma estrada reta com a velocidade escalar descrita pelo gráfico v - s . Construa o gráfico a - s .
Um avião pousa a 75m/s em uma pista reta e temm uma desaceleração descrita pelo gráfico. Determine a distância s’ percorrida antes que a sua velocidade escalar seja reduzida a 7,5 m/s. Trace o grafico
Um avião move-se ao longo de umna pista reta com uma aceleração descrita pelo gráfico. Se ele parte do repouso e precisa de uma velocidade de 90m/s para decolar, determine o comprimento de pista minim