Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 175
Uma partícula se move ao longo da espiral mostrada na figura. Determine a intensidade da velocidade da partícula em termos de b, , .
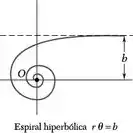
Passo 1
Espiral hiperbólica.
Do Problema 11.173
Passo 2
Como = = constante, = 0, escrevemos:
Resposta
Exercícios de Livros Relacionados
39. Levando em consideração a variação da aceleração gravitacional a com relação à altitude y ( ve Problema 12.38), deduza uma equação que relacione a velocidade de uma partícula caindo livremente com
29. A posição de uma partícula ao longo de uma linha reta é dada por s = 1,5 t 3 - 13,5 t 2 + 22,5 tm , onde t é dado em segundos. Determine a posição da partícula quando t = 6 s e a distância total q
31.A aceleração de uma partícula à medida que se move ao longo de uma linha reta é dada por a = 2 t - 1m / s 2 , onde t é dado em segundos. Se s = 1m e v = 2m/s quando t = 0, determine a velocidade da
35. Uma partícula tem velocidade escalar inicial de 27 m/s. Se ela experimenta uma desaceleração de a = - 6 tm / s 2 , onde t é dado em segundos, determine sua velocidade após ela ter viajado 10m. Qua
28. Se os efeitos da resistência atmosférica são levados em consideração, um corpo caindo tem uma aceleração definida pela equação a = 9,81 1 - v 2 10 - 4 m s 2 , onde v é dado em m/s e a direção posi