Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 59
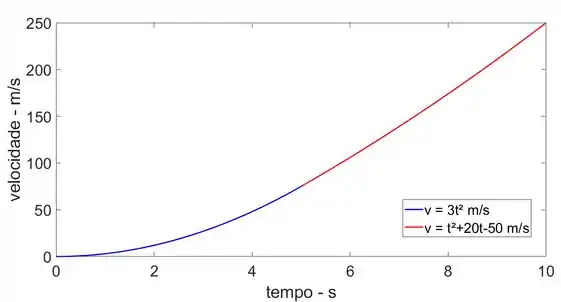
Um míssil partindo do repouso move-se ao longo de uma pista reta e por 10 s tem uma aceleração, como mostrado. Trace o gráfico v-t que descreve o movimento e descubra a distância percorrida em 10 s.
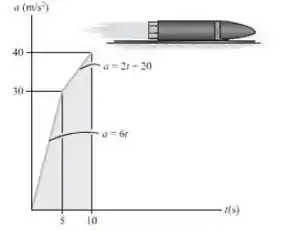
Passo 1
Para t
Quando t = 5s,
Passo 2
Para o intervalo de tempo 5
Quando t = 10 s,
Calculo da distância para t = 5 s,
Calculo da distância para t = 10 s,
Resposta
O gráfico está mostrado abaixo.
Exercícios de Livros Relacionados
Inclua a resistência do ar proporcional ao quadrado da velocidade da bola no problema anterior. Considere o coeficiente de arrasto como sendo c w = 0,5 , o raio da bola igual a 5c m e sua massa 200g .
Um cubo sólido de densidade uniforme e lados com dimensão b se encontra em equilíbrio na parte superior de um cilindro de raio R (Figura 2.C). Os planos dos quatro lados do cubo são paralelos ao eixo
Uma partícula se move em órbita bidimensional definida por: x t = A 2 α t - s e nα t y t = A ( 1 - cos α t ) Determine a aceleração tangencial at, e a aceleração normal an, como uma função do tempo,
Um canhão se localiza sobre uma elevação de altura h sobre o vale de um rio. Se a velocidade de disparo na boca do canhão é v0, determine a expressão para o alcance em função do ângulo de elevação da
Uma abóbora de massa 5 kg, lançada de um "canhão" feito por um aluno sob pressão atmosférica, em um ângulo de elevação de 45⁰, caiu a uma distância de 142 m do canhão. Os alunos utilizaram feixes de l