Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 2.Problemas - Ex. 8

Um projétil é disparado com velocidade v 0 de modo a passar entre dois pontos a uma distância h acima da horizontal. Mostre que, se a arma for ajustada para alcance máximo, a separação entre os pontos é:

d = v 0 g v 0 2 - 4 g h

Passo 1

E aí galera, vamos iniciar mais uma questão do nosso livro!

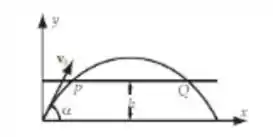
Lembrando das equações do movimento, temos:

S = v 0 t + 1 2 g t 2

v = v 0 + a t

Por substituição ao longo do eixo x temos:

x = v 0 t + 1 2 a x t 2

Se a x = 0 , nós temos:

x = v 0 cos ⁡ θ t

Dessa forma para o eixo y nós temos:

v = v 0 s in ⁡ θ a y t

Como na altura máxima v = 0 , t = t / 2 e a = - g , então temos:

v 0 sin ⁡ θ = g t 2

Portanto t = 2 v 0 sin ⁡ θ / g .

Por substituição t na equação temos:

x = v 0 cos ⁡ θ 2 v 0 sin ⁡ θ g   = 2 sin ⁡ ( θ ) cos ⁡ ( θ ) v 0 2 g = v 0 2 g sin ⁡ 2 θ

Afim de ajustar a arma para o alcance máximo, então sin ⁡ 2 θ = 1

Portanto θ = 45 °  

Então nós temos:

x = v 0 2 g

Passo 2

Agora vamos ao próximo passo, temos que:

d = x - 2 r

r = v 0 cos ⁡ θ t 2 = v 0 2

Onde t 2   é o tempo que projetil leva para atingir y = h , assim temos:

h = v 0 2 t 2 - 1 2   g t 2 2

resolvendo para t 2 , teremos:

t 2 = v 0 2 ± v 0 2 2 - 2 g h g

Por substituição, resolvendo para termos de r   teremos:

r = v 0 2 v 0 2 ±   v o 2 2 - 2 g h   g    

Por substituição para encontrar d , temos:

d = x - 2 r = v 0 2 g - v 0 2 2 g ± 2 v 0 g v 0 2 g - 2 g h =   ± v 0 g v 0 2 - 4 g h

Escolheremos para o caso a solução positiva:

d = v 0 g v 0 2 - 4 g h

Finalizamos aqui nossa questão, tudo beleza? Te vejo na próxima!

Resposta

d = v 0 g v 0 2 - 4 g h

Exercícios de Livros Relacionados

Se a motocicleta tem uma desaceleração de a t = - 0,001 sm / s 2 e sua velocidade escalar na posição A é 25m / s , determine a intensidade da sua aceleração quando ela passa o ponto B.
Um carro está se movendo ao longo da estrada com a velocidade escalar de v = ( 300 / s )m / s , onde s é dado em metros. Determine a intensidade da sua aceleração quando t = 3s se t = 0 em s = 0 .
Uma partícula move-se ao longo da trajetória parabólica y = b x 2 . Se sua componente da velocidade ao longo do eixo y é v y = c t 2 , determine as componentes x e y da aceleração da partícula. Aqui,
Uma partícula desloca-se ao longo da trajetória circular x 2 + y 2 = r 2 . Se a componente y da velocidade da partícula é v y = 2 r c o s 2 t , determine as componentes x e y da sua aceleração em qual
O jogador de beisebol A rebate a bola com v A = 12m / s e θ A = 60 ° . Quando a bola está diretamente acima do jogador B, ele começa a correr embaixo dela. Determine a velocidade escalar constante v B