Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 2.Problemas - Ex. 5

Um piloto de jato sabe que é capaz de suportar uma aceleração de 9 g   antes de perder os sentidos. Ele aponta sua aeronave verticalmente para baixo voando em velocidade Mach3 e pretende arremeter em uma manobra circular antes de colidir com o solo. (a) Onde ocorre a aceleração máxima na manobra? (b) Qual é o raio mínimo que o piloto pode utilizar?

Passo 1

Faaala meu povo, bora iniciar mais uma questão do nosso livro!

Essa questão é muito boa, vamos analisar passo a passo então vem comigo!

A partir da imagem abaixo a gente vai discutir a questão:

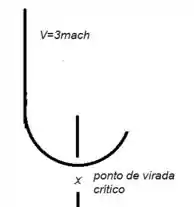
Letra (a):

Aplicando a 2º lei de Newton temos:

N - m g = m v 2 r

Portanto podemos notar que a aceleração que o piloto sente estará em seu valor máximo no ponto crítico onde a aceleração é igual a:

N m = m v 2 r + g

Passo 2

Letra (b):

Se o piloto pode levar a uma aceleração de 9 g , então nos deparamos coma seguinte desigualdade:

a = 9 g > v 2 r

Portanto a gente tem:

r > v 2 9 g = 1029 2 9 ( 9,8 ) = 12005   m

Então o raio deve ser maior que 12,005   k m

Tudo beleza? Te vejo na próxima!

Resposta

Letra (a):

a m = m v 2 r + g

Letra (b):

r > 12,005   k m

Exercícios de Livros Relacionados

25. Quando uma partícula é projetada verticalmente para cima com uma velocidade inicial de v 0 , ela experimenta uma aceleração a = - g + k v 2 , onde g é a aceleração devida à gravidade; k é uma cons
Uma bola é chutada do ponto A com a velocidade inicial v a = 10 m/s. Determine o alcance R e a velocidade escalar quando a bola tocar o solo.
Uma bola de futebol americano deve ser chutada sobre o poste do gol que fica a 4,5 m de altura. Se a sua velocidade escalar inicial é v A = 24m / s , determine se ela consegue ultrapassar o poste do g
Pacotes pequenos movendo-se sobre uma esteira transportadora caem dentro de um carrinho de carga de 1 m de comprimento. Se a esteira está se movendo com uma velocidade escalar constante de v c = 2m /
Uma bola de futebol americano é chutada sobre o poste do gol com uma velocidade de v A = 24m / s como mostrado. Determine o ponto Bx , y onde ela atinge as arquibancadas.