Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 7

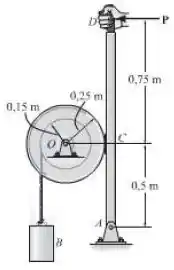
O tambor tem massa de 50   k g e raio de giração em relação ao pino em O , k O = 0,23   m . Partindo do repouso, o bloco suspenso B , de 15   k g , é deixado cair por 3   m , sem que se aplique o freio A C D . Determine a velocidade do bloco nesse instante. Se o coeficiente de atrito cinético na sapata do freio é μ k = 0,5 , determine a força P que deve ser aplicada à alavanca do freio, a qual em seguida irá parar o bloco após este haver descido outros 3   m . Despreze a espessura da alavanca.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos desenhar o diagrama de corpo livre do tambor:

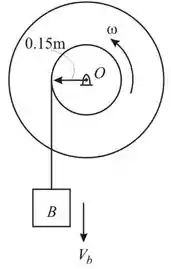
Podemos aplicar o princípio do trabalho e energia analisando o momento incial e final do sistema.

T 1 + ∑ U 1 → 2 = T 2

T 1 = 1 2 m v 1 2

Como o sistema está em repouso no momento inicial, temos que v 1 é nulo, logo:

T 1 = 0

Para o momento final, temos:

T 2 = 1 2 m v 2 2 + 1 2 I O ω 2 2

Sendo v 2 a velocidade do bloco B no final do movimento analisado, e sabendo que ω 2 = v 2 / r e I O = m O k O 2 .

Temos então que:

T 2 = 1 2 15 v B 2 + 1 2 50 0,23 2 v B 0,15 2  

T 2 = 66,3 v B 2

Passo 2

A parcela do trabalho ∑ U 1 → 2 , será:

∑ U 1 → 2 = m g h 1 - m g h 2

Lembrando que h 1 e h 2 são as alturas iniciais e finais do bloco B .

h 1 = 0

h 2 = - 3   m

Portanto:

∑ U 1 → 2 = m g ( h 1 - h 2 )

∑ U 1 → 2 = 15 9,81 0 - - 3

∑ U 1 → 2 = 441,45

Agora é só aplicar:

T 1 + ∑ U 1 → 2 = T 2

0 + 441,45   = 66,3 v B 2

v B = 2,58   m / s

Passo 3

A partir da análise do aspecto construtivo do tambor, temos que:

s B 0,15 = s C 0,25

Como dito no enunciado, s B = 3   m , logo:

s C = 0,25 0,15 3

s C = 5   m

Passo 4

Vamos aplicar o princípio do trabalho e energia novamente após acionar o freio:

T 1 + ∑ U 1 → 2 = T 2

0 - F 5 + 15 9,81 6 = 0

F = 176,6   N

N = 176,6 0,5

N = 353,2   N

Aplicando o momento em A , para saber a força P aplicada, temos:

∑ M A = 0

- 353,2 0,5 + P 1,25 = 0

P = 141   N

Resposta

v B = 2,58   m / s

P = 141   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma força de 20N é aplicada ao cabo que faz a bobina de raio de giração rg=0,42m e massa de 175kg girar sobre os rolos A e B, sem deslizar. Determinar sua velocidade angular ao completar duas revoluçõ
O pêndulo da máquina de impacto Charpy com massa de 50 kg e raio de giração ka=1,75m é solto quando θ=0°. Determinar sua velocidade angular logo antes de atingir o corpo de prova S, onde θ=90°.
Em um dado instante, o corpo de massa m com uma velocidade angular ω e uma velocidade de seu centro de massa vg. Demonstrar que sua energia cinética total se dá por T = 1 2 . I i c . ω ² ², onde Iic é
Os dois rebocadores exercem uma força de intensidade F cada uma, sobre o navio de massa m e raio de giração kg, que estão sempre direcionadas perpendicularmente a linha central do navio. Determinar su
O motor elétrico apresentado está fornecendo 4k W a 1725r p m para uma bomba a qual aciona. Calcule o ângulo δ por meio do qual o motor se inclina sob a ação da carga, se a rigidez de cada uma de suas