Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 36
A partícula 1 é submetida a uma aceleração , a partícula 2 é submetida a , e a partícula 3 é submetida a . Todas as três partículas partem da origem com uma velocidade inicial no instante , e o módulo de é para todas as três partículas (note que as unidades de variam de caso para caso). Represente graficamente a posição, a velocidade e a aceleração contra o tempo para cada partícula durante o intervalo .
Passo 1
Vamos lá, nosso objetivo é encontrar as expressões para posição, velocidade e aceleração em função do tempo para cada um dos casos.
Começamos com o caso em que . Vamos usar a definição da aceleração:
Vamos integrar dos dois lados:
Beleza, essa é a velocidade, agora é só integrar para achar a posição (sabendo que ).
Essa é a posição, agora é só derivar a velocidade para achar a aceleração:
Excelente, vamos para a próxima partícula.
Passo 2
Agora a expressão para aceleração é . Esse caso vai ser bem mais fácil, porque já estamos trabalhando com funções do tempo.
E agora é só integrar de novo para achar a posição! (Lembrando que )
Ótimo, vamos para a próxima.
Passo 3
Agora a expressão para aceleração é . Dessa vez precisamos fazer algo um pouco mais complicado:
Substituindo a expressão:
E integrando:
Mas isso ainda está em função da posição, queremos alguma coisa em função do tempo!
(Por simplicidade vamos ocultar esse agora, depois voltamos a ele):
E integrando:
E agora o desafio é resolver essa integral.
Passo 4
Vamos começar reorganizando:
E essa é uma integral conhecida:
Então:
Vamos usar , já que a constante deve estar associada à posição inicial, que é nula.
Agora vamos isolar a velocidade:
Agora podemos derivar para achar a velocidade:
E derivando mais uma vez chegamos na aceleração:
OBS: Lembra daquele que deixamos lá em cima? Como a velocidade inicial é positiva, sabemos que a posição inicial deve crescer logo que o movimento se inicia, então as soluções obtidas estão corretas.
Passo 5
Então agora vamos rever os resultados e substituir os valores para fazer os gráficos.
Em todos os gráficos a curva vermelha representa , a curva é azul e a curva é verde.
Para as posições temos:
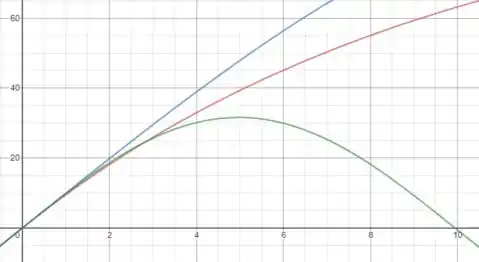
Para as velocidades temos:
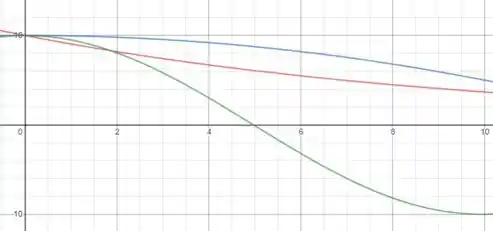
E para as acelerações temos:
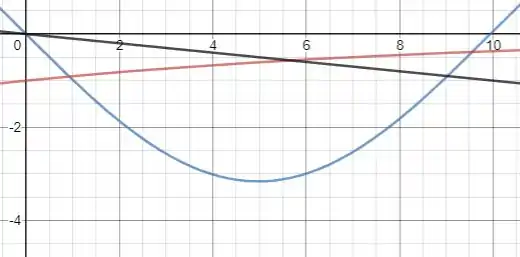
Resposta
As equações da posição são: , , .
As equações da velocidade são: , , .
As equações da aceleração são: , , .