Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 57

Repita o Prob. 2/56, porém agora inclua os efeitos do arrasto aerodinâmico. As forças de arrasto provocam uma componente de aceleração em m / s 2 de 0,016 v 2 na direção oposta ao vetor velocidade, onde v é em m / s .

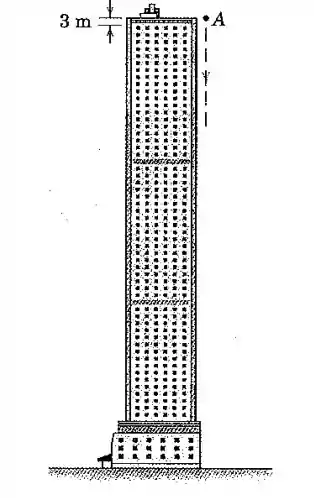
Prob. 2/56: Os pavimentos de um edifício alto são uniformemente espaçados de 3 metros de altura. Uma bola A é deixada cair da posição mostrada do telhado. Determine os tempos necessários para que esta passe os 3 metros do primeiro, décimo e centésimo andares (contados a partir do topo). Despreze o arrasto aerodinâmico.

Passo 1

Pessoal, considerando o arrasto aerodinâmico, a aceleração será:

a = g - k v 2

Podemos usar então a seguinte equação diferencial:

a   d t = d v

g - k v 2   d t = d v

d t = 1 g - k v 2   d v

Vamos integrar cada lado:

∫ 0 t d t = ∫ 0 v 1 g - k v 2   d v

Consultando uma tabela de integrais, obtemos:

t = 1 g k tanh - 1 ⁡ k g v 0 v

t = 1 g k tanh - 1 ⁡ k g v

Passo 2

Fazendo umas manipulações, obtemos v em função de t :

g k   t = tanh - 1 ⁡ k g v

tanh ⁡ g k   t = k g v

v = g k   tanh ⁡ g k   t

Agora sim, podemos usar a seguinte equação diferencial:

d y = v   d t

d y = g k   tanh ⁡ g k   t   d t

∫ 0 y d y = g k   ∫ 0 t tanh ⁡ g k   t   d t

Consultando mais uma vez uma tabela de integrais, obtemos:

y = 1 k ln ⁡ cosh ⁡ g k   t

Passo 3

Agora vamos manipular a equação, para ela nos dar t em função de y :

k y = ln ⁡ cosh ⁡ g k   t

e k y = cosh ⁡ g k   t

cosh - 1 ⁡ e k y = g k   t

t = 1 g k cosh - 1 ⁡ e k y

Como temos g = 9,81   m / s 2 e k = 0,016   m - 1 , obtemos:

t = 2,53 cosh - 1 ⁡ e 0,016   y

Vamos agora usar essa função para calcular os tempos de chegada em cada andar, organizando os dados na tabela a seguir:

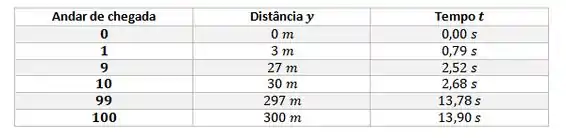
Então, para a bola passar os 3 metros do primeiro andar, temos:

Δ t 1 = t 1 - t 0 = 0,79 - 0,00 = 0,79   s

Para passar os 3 metros do décimo andar, o tempo será:

Δ t 10 = t 10 - t 9 = 2,68 - 2,52 = 0,16   s

E por último, para o centésimo andar, teremos:

Δ t 100 = t 100 - t 99 = 13,90 - 13,78 = 0,12   s

Resposta

Δ t 1 = 0,79   s

Δ t 10 = 0,16   s

Δ t 100 = 0,12   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

32. A bola A é jogada verticalmente para cima do topo de um prédio de 30m com uma velocidade inicial de 5 m/s. No mesmo instante, outra bola B é jogada para cima a partir do chão com uma velocidade in
36. A aceleração de uma partícula movendo-se ao longo de uma linha reta é a = 8 - 2 sm / s 2 , onde s é dado em metros. Se v = 0e ms = 0 , determine a velocidade da partícula em s = 2m e a posição da
27. Uma partícula move-se ao longo de uma linha reta com uma aceleração de a = 5 3 s 1 3 + s 5 2m / s 2 , onde sé é dado em metros. Determine a velocidade da partícula quando s = 2m, se ela partir do
34. Uma partícula move-se ao longo de uma linha reta com uma velocidade v = 200 sm m / s , onde s está indicado em mm. Determine a aceleração da partícula em s = 2000 mm. Quanto tempo leva para a part
30. A velocidade de uma partícula movendo-se ao longo de uma linha reta é v = v 0 - k s , onde k é constante. Se s = 0 quando t = 0, determine a posição e a aceleração da partícula como uma função do