Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 212

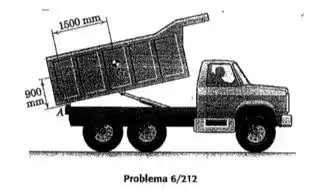
O caminhão basculante transporta 5   m 3 de terra com uma massa especifica de 1600   k g / m 3 , e o mecanismo de elevação gira a caçamba em torno da articulação A a uma velocidade angular constante de 4graus/s. O centro de massa da caçamba e da carga está em G. Determine a potência máxima P necessária durante a inclinação da carga.

Passo 1

A potência máxima necessária será dada no momento em que a caçamba está no inicio do movimento, já que a terra está toda distribuída pelo volume da caçamba (em outros momentos, a terra terá se deslocado para perto do eixo, o que fará com que o centro de massa se desloque para perto do eixo, e o momento gerado pela força gravitacional será menor, pois o braço de momento é menor). Pela equação da velocidade do centro de massa: v y = ω r

Passo 2

E pela equação da potência:

P = m g ω r = ρ V g ω r

Substituindo os valores das grandezas:

P = 1600 k g / m 3 ( 5 m 3 ) 9.81 m / s 2 4 ° π 180 ( 1.500 m )

P = 8.22 k W

Resposta

P = 8.22 k W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As pequenas esferas, que possuem as massas e velocidades iniciais indicadas na figura, atingem e tornam-se presas às extremidades pontudas da haste, que é livremente articulada em O e está inicialment
Em um dado instante, a partícula de massa m tem a posição e a velocidade mostradas na figura, e sofre a ação da força F . Determine sua quantidade de movimento angular em torno do ponto O e a taxa de
O conjunto parte do repouso e atinge uma velocidade angular de 150r p m sob a ação de uma força T de 20N aplicada à corda por t segundos. Determine t . Despreze o atrito e todas as massas exceto a das
Um elemento de máquina é suportado por molas e está ligado a umamortecedor como mostrado na figura. Mostre que, se uma força periódica de intensidade P = P ms e nω ƒ t , ƒ é aplicada ao elemento, a am
Um modelo simplificado de uma máquina de lavar é mostrada na figura. Uma trouxa de roupa molhada forma uma massa m b de 10 kg na máquina e causa um desbalanceamento rotativo. A massa rotativa é 20 kg