Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 217
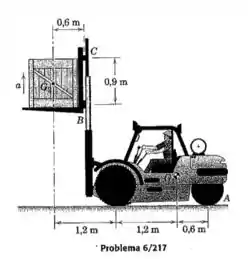
A empilhadeira com centro de massa em possui uma massa de , incluindo o mastro vertical. O garfo e a carga têm uma massa combinada de , com centro de massa em . A guia rolante em é capaz de suportar apenas força horizontal enquanto a conexão em além de suportar a força horizontal, também transmite a força de elevação vertical. Se o garfo recebe uma aceleração ascendente, que é suficiente para reduzir a força sob as rodas traseiras em para zero, calcule a reação correspondente em .
Passo 1
Vamos utilizar a equação dos momentos para um ponto E que está exatamente sob a roda maior da empilhadeira, na pequena reta vertical entre os dois valores de 1,2m de comprimento no desenho do enunciado. A equação será:
E os momentos serão os momentos gerados pela força gravitacional sobre os dois centros de massa
O d do final da equação, corresponde à distância do ponto N até a reta que passa pelo vetor , ou seja, . E a massa é a massa da carga com o garfo.
Passo 2
Vamos isolar a aceleração:
E substituir o valor de cada grandeza:
Passo 3
Agora vamos utilizar novamente a mesma equação, mas agora em relação ao ponto C:
Os momentos envolvidos, dessa vez serão apenas a força gravitacional da carga e a força da guia rolante no ponto B, que suporta apenas força horizontal, e portanto, a força exercida sobre a carga será horizontal e a força será perpendicular à distancia entre B e C. A equação fica:
Isolamos a força
E como a aceleração será a mesma do caso anterior, já que ainda estamos escrevendo em relação ao movimento da carga, podemos substituir todos os valores: