Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 54
Use o valor de citado na resposta do Prob. 2/53 e determine o tempo necessário para o piloto de drag race descrito naquele problema completar os da corrida.
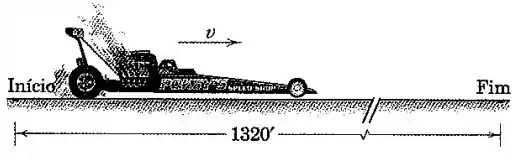
Prob. 2/53: A aceleração do piloto de drag race é modelada como , onde o termo leva em consideração o arrasto aerodinâmico e onde e são constantes positivas. Se é conhecido (a partir de testes no túnel de vento) como , determine se a velocidade final é . Uma drag race é uma corrida em pista reta de que inicia do repouso.
Passo 1
Pessoal, pra calcular o tempo e usar a constante já conhecida, temos que trabalhar com uma equação diferencial que contenha a aceleração . Como a aceleração está em termos da velocidade, a melhor equação diferencial pra se usar é:
Substituindo o valor de :
Passo 2
Show! Agora é só integrar a equação, lembrando que :
Se consultarmos uma tabela de integrais, veremos que:
Se substituirmos os valores das constantes e , teremos: