Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 60

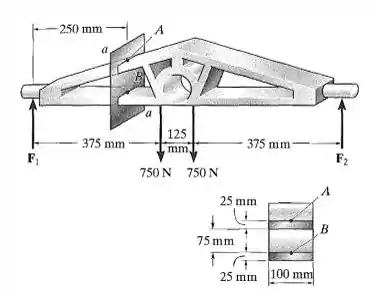
A peça fundida cônica suporta a carga mostrada. Determine a tensão de flexão nos pontos A e B. A seção transversal na seção a-a é dada na figura.

Passo 1

Por simetria, sabemos que:

F 1 = F 2 = 750 N

Logo, o momento na seção será:

∑ M = 0 → M - 0,25 × 750 = 0

M = 187,5 N m

O momento de inércia da seção é dado por:

I = 0,1 × 0,125 3 12 - 0,1 × 0,075 3 12 = 1,276041   × 10 - 5

Passo 2

Agora, podemos calcular as tensões:

σ a = 187,5 × 0,0625 1,276041   × 10 - 5 = 0,918 M P a

σ b = 187,5 × 0,0375 1,276041   × 10 - 5 = 0,551 M P a

Resposta

σ a = 0,918 M P a

σ b = 0,551 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um elemento de máquina de alumínio fundido e na forma de um sólido de revolução de diâmetro variável d está sendo projetada para suportar a carga mostrada. Sabendo que o elemento da máquina deve ser d
Trace os diagramas de força cortante e o momento fletor para a viga e carregamento mostrados, e determine o valor máximo absoluto ( a ) da força cortante e momento fletor e ( b ) do momento fletor.
Para a viga e carregamento mostrados, ( a ) trace os diagramas de força cortante e momento fletor e ( b ) determine as equações das curvas de força cortante e momento fletor.
Para a viga e carregamento mostrados, ( a ) trace os diagramas de força cortante e momento fletor e ( b ) determine as equações das curvas de força cortante e momento fletor.
Para a viga e carregamento mostrados, ( a ) trace os diagramas de força cortante e momento fletor e ( b ) determine as equações das curvas de força cortante e momento fletor.