Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 53
O tubo de retorno com descarrega água salgada (massa específica de ) no ambiente a uma taxa constante de . A pressão estática da água na seção é de acima da pressão atmosférica. A área do escoamento no tubo em é e em cada uma das duas saídas é . Se cada um dos seis parafusos no flange é apertado com uma chave de torque de modo a ser submetido a uma tração de , determine a pressão média sobre a vedação entre os dois flanges. A área do flange em contato com a vedação é . Determine também o momento fletor na seção do tubo quando a descarga do lado esquerdo é obstruída e a sua vazão é reduzida à metade. Depreze o peso do tubo e da água em seu interior.
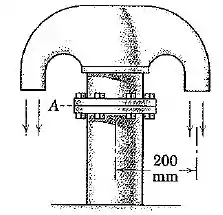
Passo 1
Bom, logo de cara o enunciado já nos deu um valor bastante importante: o volume de água por unidade do tempo que circula no sistema:
A partir de , podemos calcular também a taxa de escoamento de massa :
Como também conhecemos a área de cada um dos tubos de saída e a área do tubo principal, podemos calcular as velocidades nesses dois pontos:
Passo 2
E agora podemos usar a fórmula da força resultante para calcular a força a que os flanges tem que resistir:
Lembre sempre de projetar as velocidades no eixo em questão. No nosso caso, definimos o sentido vertical para cima como positivo.
Agora vamos pensar na soma das forças:
O primeiro termo é a pressão vinda do tubo principal, o segundo se refere à pressão vinda dos parafusos apertados com a chave de torque, e a terceira é a pressão que queremos caclaular.
Passo 3
Se obstruírmos um dos lados, a vazão do sistema é reduzida pela metade:
E a taxa de escoamento de massa é:
Nesse caso, a velocidade no tubo que ficou aberto passa a ser:
E agora é só aplicar a fórmula para o momento fletor:
Resposta
A pressão média é e o momento é .