Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 22

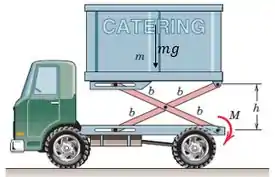
A caixa de carga do caminhão de entrega de alimentos para aeronaves a manutenção tem uma massa carregada m e é elevada pela aplicação de um torque M na extremidade inferior do elo que é articulado à estrutura do caminhão. A ranhura horizontal permite que a ligação se desdobre conforme a carga a caixa é elevada. Expresse M como uma função de h.

Fonte: Meriam - Estática - 7ª ed

Passo 1

Fala aí gente top!

Vamos com tudo pra mais um probleminha haha!

Primeiro, o problema é bem direto, quer a expressão de M como uma função de h.

E, fazendo o diagrama do corpo livre, percebemos que há, além do momento M, a força peso da caixa de carga:

Passo 2

Assim, aplicando o princípio do trabalho virtual:

δ U = 0 ;                 M δ θ - m g δ h = 0                                           ( 1 )

Por geometria, o deslocamento h causado pelo peso da carga pode ser encontrado como:

h = 2 b s e n θ                         → δ h = 2 b c o s θ δ θ    

Assim, podemos substituir na eq. 1:

  M δ θ - m g 2 b c o s θ δ θ = 0                       → δ θ M - m g 2 b c o s θ = 0

Rearranjando termos, temos:

M = m g 2 b c o s θ

Passo 3

Já encontramos a expressão do momento M, porém o problema nos pede que esse seja em função de h. O que podemos fazer?

Bem, pela geometria da figura do problema, podemos relacionar h com o ângulo θ :

s e n θ = h 2 b   ;                 s e n 2 θ + cos 2 ⁡ θ = 1                   → c o s θ = 1 - h 2 b 2    

Agora, podemos substituir a expressão do c o s θ na equação do momento M:

M = m g 2 b 1 - h 2 b 2

Resposta

Portanto

M = m g 2 b 1 - h 2 b 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A caçamba do caminhão de entrega de alimentos para aeronaves tem massa m quando carregada e é levantada pela aplicação de um torque M na extremidade inferior da engrenagem, que é articulada com a estr
Determine o momento M que deve ser aplicado em O para sustentar o mecanismo na posição θ = 30 ° . As massas do disco em C , da barra O A e da barra B C são m 0 , m e 2 m , respectivamente.
Na morsa acionada por um parafuso, um torque M aplicado à manopla do parafuso aperta a morsa aumentando a distância B D e, portanto, produzindo uma força de aperto C . O parafuso é rosqueado através d
Uma “caixa preta” contém uma série de cremalheiras e pinhões, engrenagens e outros elementos mecânicos internos interconectados, os quais transformam o movimento linear da haste A em um movimento line
A barra leve O C é articulada em O e balança no plano vertical. Quando θ = 0 , a mola de rigidez k não está alongada. Determine o ângulo de equilíbrio, correspondente a uma força vertical P aplicada à