Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 55
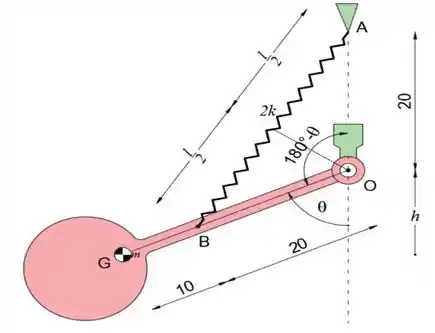
O pêndulo de 3 lb oscila em torno do eixo OO e tem um centro de massa em G. Quando θ = 0, cada mola tem um alongamento inicial de 4 pol. Calcule a rigidez máxima k de cada uma das molas paralelas que permitirá que o pêndulo seja em equilíbrio estável na posição inferior θ = 0.
Passo 1
Observe que não há forças externas atuando no sistema, portanto, podemos escrever a equação de equilíbrio como
(1)
Podemos ver pelo esboço que metade do comprimento da mola é
Portanto, o comprimento total da primavera é
Passo 2
Observe que quando θ = 0, a mola está 4 pol. Esticada e seu comprimento é
O que significa que o comprimento da mola não esticada é
Sabendo disso, podemos escrever a mudança no comprimento da mola como
Também podemos ver que a mudança na altura h é
Passo 3
Escreveremos a expressão da energia potencial gravitacional
Substituiremos h por
Derivaremos ambos lados da equação
(2)
Uma vez que temos duas molas acopladas, e escrevemos a mudança no comprimento da mola como Δl, podemos escrever a expressão para a energia potencial elástica como
Substituiremos por
Derivaremos ambos lados da equação
Passo 4
Em seguida, vamos substituir δVg e δVe pelas expressões (2) e (3) na equação
Observe que, para que o sistema esteja em equilíbrio, a segunda derivada da equação de equilíbrio precisa ser maior que zero
Para verificar a estabilidade de θ = 0, vamos simplesmente colocar o valor de θ na expressão (4)
Expressaremos k como
Substituiremos g por seus valores
Para que o sistema seja estável em θ = 0, a rigidez k não pode ser maior que 1,104 lb / in., Portanto, podemos dizer que a rigidez máxima k que garantirá a estabilidade é