Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 11.Problemas - Ex. 22

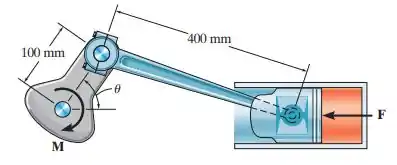
O virabrequim está sujeito a um torque M = 50   N · m . Determine a força compressiva horizontal F e faça o gráfico de F (ordenada) versus θ , (abscissa) para 0 ≤ θ ≤ 9 0 ° .

Passo 1

Fala aí, galerinha do Responde aí. Tudo beleza? Vamos fazer mais uma questão de Estática.

Este problema nos pede para determinarmos a força compressiva horizontal F aplicada ao pistão para o equilíbrio quando θ = 60 ° . Primeiro, vamos utilizar a equação de trabalho virtual de modo que:

0,4 2 = 0,1 2 + x 2 - 2 0,1 x cos ⁡ θ 0 = 0 + 2 x δ x + 0,2 x sin ⁡ θ   δ θ - 0,2 cos ⁡ θ   δ θ δ x = 0,2 x sin ⁡ θ 0,2 cos ⁡ θ - 2 x δ θ

δ U = 0 ;       - 50 δ θ - F δ x = 0

Assim, a força compressiva horizontal F aplicada ao pistão vai ser:

- 50 δ θ - F 0,2 x sin ⁡ θ 0,2 cos ⁡ θ - 2 x δ θ = 0 ,                 δ θ ≠

= 0 F = 50 2 x - 0,2 cos ⁡ θ 0,2 x sin ⁡ θ

Passo 2

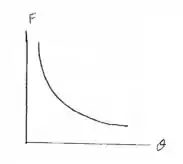
Para esboçarmos o gráfico, temos a partir da equação da força que:

x 2 - 0,2 x cos ⁡ θ - 0,15 = 0 x = 0,2 cos ⁡ θ ± 0,04 cos 2 ⁡ θ + 0,6 2 ,     d e s d e   q u e   0,04 cos 2 ⁡ θ + 0,6 > 0,2 cos ⁡ θ

Logo:

x = 0,2 cos ⁡ θ + 0,04 cos 2 ⁡ θ + 0,6 2

Assim, a força neste intervalo vai ser:

F = 50 0,04 cos 2 ⁡ θ + 0,6 0,2 cos ⁡ θ + 0,04 cos 2 ⁡ θ + 0,6 + 0,6 sin ⁡ θ

Esboçando o gráfico, temos:

É isso, galera, Bora resolver mais questões pra ficar craque.

Resposta

F = 512 N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A prensa perfuradora consiste em um cilindro R , barra de conexão A B e um volante. Se um torque de M = 50 N ⋅ m for aplicado ao volante, determine a força F aplicada no cilindro para manter a barra n
Determine a intensidade do momento de binário M necessário para suportar o cilindro de 20 k g na configuração mostrada. A ranhura lisa em B pode deslizar livremente dentro da ranhura. Despreze a massa
A barra uniforme A B tem um peso de 50 N . Se a mola D C está livre quando θ = 0 ° , determine o ângulo θ para o equilíbrio usando o princípio do trabalho virtual. A mola sempre permanece na posição h
As ligações uniformes A B e B C pesam cada uma 10 N e o cilindro pesa 100 N . Determine a força horizontal P necessária para manter o mecanismo em θ = 45 ° . A mola tem um comprimento livre de 150 m m
O virabrequim está sujeito a um torque M = 75 N ⋅ m . Determine a força compressiva vertical F aplicada ao pistão para o equilíbrio quando θ = 60 ° .