Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 19.Problemas - Ex. 6

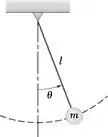
Um pêndulo simples consistindo de um peso ligado a uma corda oscila em um plano vertical com um período de 1,3 s. Considerando um movimento harmônico simples e sabendo que a velocidade máxima do pêndulo é de 400 mm/s, determine (a) a amplitude do movimento em graus, (b) a aceleração tangencial máxima do peso.

Passo 1

Partiu mais uma questão de resmat :D

O exercício pede que a gente determine a amplitude do movimento em graus, (b) a aceleração tangencial máxima do peso.

  1. Movimento harmônico simples é dado por:

    2. θ = θ m sin ⁡ ω n t + ϕ

    ω n = 2 π τ n = 2 π 1.3   s

    ω n = 4.833   rad/s

    θ ˙ = θ m ω n cos ⁡ ω n t + ϕ

    θ ˙ = θ m ω n

    v m = l θ ˙ m = l θ m ω n

    θ m = v m l ω n

    Passo 2

    Consideramos para um pêndulo simples,

    ω n = g l

    Portanto,

    l = g ω n 2 = 32.2   ft/ s 2 4.833   rad/s 2

    l = 1.378   ft

    Passo 3

    Amplitude.

    Da Eq. (1),

    θ m = v m l ω n = 15 12   ft/s 1.378   ft 4.833   rad/s

    θ m = 0.18769   rad

  2. Aceleração tangencial máxima.

a t = l θ ¨

A aceleração tangencial máxima ocorre quando θ ¨ é o máximo.

θ ¨ = - θ m ω n 2 sin ⁡ ω n t + ϕ

θ ¨ max = θ m ω n 2

a t max = l θ m ω n 2

a t max = 1.378   ft 0.1879   rad 4.833   rad/ s 2 = 6.04   ft/ s 2

Resposta

a )   θ m = 10.75 °

b )   a t m = 6.04   ft/ s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O movimento da haste delgada de 10 kg AB é guiado por colares de massa desprezível que deslizam livremente nas hastes verticais e horizontais mostradas. Sabendo que a barra é solta do repouso quando θ
Dois cilindros uniformes, cada um com peso W = 14 lb e raio r = 5 pol., São conectados por uma correia, conforme mostrado. Se o sistema for liberado do repouso, determine (a) a velocidade do centro do
A haste de 5 kg BC é presa por pinos a dois discos uniformes, conforme mostrado. A massa do disco de raio de 150 mm é de 6 kg e a do disco de raio de 75 mm é de 1,5 kg. Sabendo que o sistema foi liber
Um colar B, de massa m e de dimensão desprezível, é preso à borda de um aro de mesma massa m e de raio r que rola sem deslizar sobre uma superfície horizontal; Determine a velocidade angular ω 1 do ar
Duas hastes uniformes, cada uma com massa m e comprimento L, são conectadas para formar a articulação mostrada. A extremidade D da haste BD pode deslizar livremente na fenda horizontal, enquanto a ext