Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 171
A pequena arruela desliza para baixo na corda OA. Quando ela está no meio do caminho, sua velocidade escalar é 200 mm/s e sua aceleração é 10mm/s². Expresse a velocidade e a aceleração da arruela nesse ponto em termos das suas componentes cilíndrincas.
Passo 1
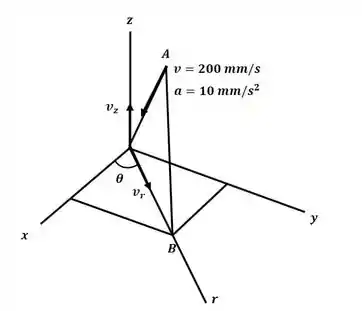
Começaremos o exercício encontrando o valor das distâncias OA e da sua projeção no plano xy com base no diagrama a seguir:
Passo 2
Agora iremos encontrar os valores para as componentes da velocidade:
Passo 3
Agora podemos calcular as componentes da aceleração:
Resposta
Exercícios de Livros Relacionados
Solucione o Problema 12.190 se a partícula tiver uma aceleração angular de θ ¨ = 5r a d / s 2 quando θ ˙ = 4r a d / s a θ = π / 2r a d .
A superfície parcial da came é uma espiral logarítmica r = 40 e 0,05 θm m , onde θ é dado em radianos. Se a came gira a uma velocidade angular constante de θ ˙ = 4r a d / s , determine as intensidades
A fenda do braço A B impulsiona o pino C pela fenda espiral descrita pela equação r = 1,5 θ m , onde θ é dado em radianos. Se p braço sai do repouso quando θ = 60 ° e é impulsionado a uma velocidade a
Determine a velocidade escalar do bloco A se a extremidade B da corda é puxada para baixo com uma velocidade escalar de 1,5m / s .
Determine a velocidade escalar do bloco A se a extremidade B da corda é puxada para baixo com uma velocidade escalar de 6m / s .