Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 22

A barra fina tem uma massa m e está suspensa em sua extremidade A por uma corda. Se a barra recebe um golpe horizontal dando a ela um impulso I em sua parte de baixo B, determine a localização y do ponto P em torno do qual a barra parece girar durante o impacto.

Passo 1

Começaremos o exercício aplicando o princípio do impulso e do momento angular ao redor do centro de massa G da barra:

↺ +   I G ω 1 + ∑ ∫ t 1 t 2 M G d t = I G ω 2

0 + I l 2 = 1 12 m l 2 ω

I = 1 6 m l ω

Passo 2

Agora podemos aplicar o princípio do impulso e da quantidade de movimento linear na direção x para obter a velocidade do centro de massa da barra:

+ →   m v A x 1 + ∑ ∫ t 1 t 2 F x d t = m v A x 2

0 + 1 6 m l ω = m v G

v G = l 6 ω

Passo 3

Agora, com o auxílio da figura a seguir, poderemos aplicar semelhança de triângulos para obter o valor de y.

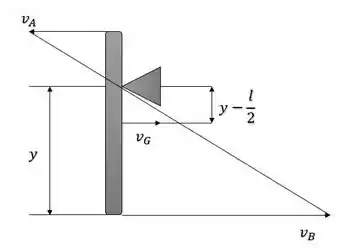
Sendo assim:

v B y = v G y - l / 2  

Mas, sabemos que a velocidade em B pode ser escrita em função da velocidade angular e do braço de alavanca:

v B = ω y

Subsituindo essa relação e o valor de v G na semelhança de triângulos:

ω y y = l 6 ω y - l / 2  

y = 2 3 l

Resposta

y = 2 3 l

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um jogador de beisebol, ao pegar uma bola, pode amortecer o impacto levando sua mão para trás. Considerando que uma bola de 140g atinge sua luva a 140k m / h e que o jogador puxa sua mão para trás dur
A fim de testar a resistência ao impacto de uma corrente, ela é suspensa por uma viga rígida de 120k g apoiada em duas colunas. Uma barra presa no último elo é, então, golpeada por um bloco de 30k g q
Uma bala de massa m é atirada com velocidade v 0 formando um ângulo com a horizontal e se aloja em um bloco de madeira de massa M . O bloco pode rolar sem atrito no piso duro e é impedido por molas de
Uma bolinha de 50 g atirada verticalmente por uma pistola de mola na superfície da Terra atinge a altura de 100 m. A mesma bolinha atirada pela mesma pistola na superfície da Lua atinge a altura de 68
Um satélite descreve uma órbita elíptica sobre um planeta de massaM. Os valores mínimos e máximos da distânciardo centro do satélite ao planeta são, respectivamente,r0er1. Use os princípios de conserv