A pequena balança postal consiste em um contrapeso W 1 , conectado aos elementos que possuem peso desprezível. Determine o peso W 2 que está na bandeja em termos dos ângulos θ e ϕ e das dimensões mostradas. Todos os elementos estão conectados por pinos.

W 2 = W 1 b a sen ⁡ θ cos ⁡ ϕ

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 11.Problemas - Ex. 45

A pequena balança postal consiste em um contrapeso , conectado aos elementos que possuem peso desprezível. Determine o peso que está na bandeja em termos dos ângulos e e das dimensões mostradas. Todos os elementos estão conectados por pinos.

Passo 1

Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!

O enunciado nos pede para determinar o peso em termos de , , e , necessário para o equilíbrio da balança com o contrapeso .

Então bora lá! Para resolver esse problema, vamos começar analisando o diagrama de corpo livre:

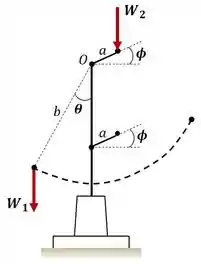
Passo 2

Show de bola! Em um primeiro momento pode parecer complexo, mas uma vez que a balança está em equilíbrio, o momento causado pelo peso em torno do eixo deve ser equivalente ao momento causado pelo contrapeso em torno desse mesmo eixo . Sendo assim, fazendo o equilíbrio de momentos em torno deste ponto:

É só isso, galera. Dá pra acreditar? Hahaha

Partiu pra próxima!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força P que deve ser aplicada à corda enrolada no tambor em C necessária para levantar o balde tendo uma massa m . Observe que, enquanto o balde é levantado, a polia enrola uma corda no ei

A barra uniforme A B pesa 500 N . Se as duas molas D EeB C estão livres quando θ = 90 ° , determine o ângulo θ para equilíbrio usando o princípio da energia potencial. Investigue a estabilidade na pos

Usando o método da Seção 10.8, resolva o Problema 10.33.

Utilizando o método da seção 10.8, resolva o problema 10.39. Determine a estabilidade da estrutura. (Dica: A energia da mola é 1 2 k θ ² ) ²

Desprezando o peso dos blocos, determine a equação em termos de θ ,W ,lek que deve ser sitisfeita para que o sistema esteja em equilíbrio. Considere a mola indeformada quando a barra é horizontal.