Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 61
Usando o método da Seção 10.8, resolva o Problema 10.33.
Passo 1
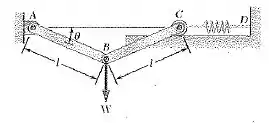
Para resolver este problema indico resolver o problema 10.33, que pode ser visualizado no site.
A partir da análise feita do problema 10.33, e utilizando energia potencial, teremos:
Passo 2
Substituindo os valores, temos que:
Resolvendo teremos:
Resposta
Exercícios de Livros Relacionados
Determine os ângulos θ para haver equilíbrio do cilindro de 50 kg e investigue a estabilidade em cada posição. A mola está livre quando θ = 60 º º
A xícara tem um fundo hemisférico e uma massa m. Determine a posição h do centro de massa G de modo que a xícara esteja em equilíbrio indiferente.
O caminhão tem uma massa de 200 Mg e um centro de massa G. Determine o grau de inclinação ao longo do qual ele possa estacionar sem tombar e investigue a estabilidade nessa posição.
A barra uniforme OA tem um peso de 100 N e quando ela está na posição vertical, a mola está livre. Determine a posição θ para o equilíbrio. Investigue a estabilidade na posição de equilíbrio.
A barra uniforme tem um peso W . Determine o ângulo θ para o equilíbrio. A mola está livre quando θ = 90 ° . Despreze o peso dos roletes.