Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 192

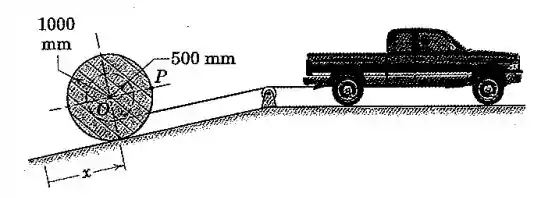
O grande carretel para cabo de eletricidade é rolado para cima no plano inclinado pelo veículo conforme mostrado. O veículo parte do repouso com x = 0 para o carretel e acelera na taxa constante de 0,6 m/s². Para o instante em que x = 1,8 m, calcule a aceleração do ponto O sobre o carretel na posição indicada.

Passo 1

Bom pessoal, considerando o rolamento sem deslizamento, temos que o ponto de contato do carretel com o solo é o Centro Instantâneo C. Além disso, a aceleração do veículo é a mesma do cabo. Desta forma, podemos calcular a aceleração no centro do carretel O.

Então temos que:

a A = 0,5 1 a O

a O = 0,6 0,5 = 1,2   m / s 2

Agora, podemos usar a equação cinemática de Torricelli para saber qual é a velocidade do centro do carretel depois de percorridos 1,8m. Lembrando que o sistema parte do repouso:

v O 2 = 2 a O x = 2 1,2 1,8 = 4,32

v O = 2,08   m / s

Passo 2

Agora, vamos usar a equação da aceleração relativa entre os pontos P e O:

a P = a O + a P O n + a P O t

Onde:

a P O n =   ω × ω × r P O = - ω 2 r P O = - v O 2 r P O = - 2,08 2 1 i = - 4,32   i ^   m / s 2

a P O t = α × r P O = - a O j ^ = - 1,2 j ^   m / s 2

Substituindo os valores na equação, temos que:

a P = 1,2 i ^ - 4,32 i ^ - 1,2 j ^ = - 3,12 i ^ - 1,2 j ^ m / s 2

Caso queria saber o módulo:

a P = - 1,2 2 + - 3,12 2 = 3,34   m / s 2

Resposta

a P = 3,34   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O disco semicircular de massa m e raio r é liberado a partir do repouso em θ = 0 e gira livremente no plano vertical em relação ao seu mancal fixo em O . Desenvolva expressões para as componentes n e
O disco B possui uma massa de 22k g e um raio de giração centroidal de 200m m . A unidade de potência C é composta por um motor M e um disco em A , que é acionado a uma velocidade angular constante de
A chapa em ângulo reto é fabricada a partir de uma chapa plana com massa ρ por unidade de área e está soldada no eixo horizontal montado no mancal em O . Se o eixo é livre para girar, determine a acel
Cada uma das hastes esbeltas uniformes de massa m está soldada na sua extremidade em uma posição tangente à borda do disco circular. O disco gira em um plano horizontal em torno de um eixo vertical fi
O dispositivo robótico é composto pela base estacionária O A , o braço articulado em A , e o braço B C articulado em B . Os eixos de rotação são perpendiculares ao plano da figura. Calcule (a) o momen